Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 53
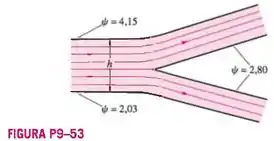
Um cálculo de CFD de escoamento permanente, incompressível, bidimensional através de uma ramificação de duto assimétrica bidimensional revela o padrão de linhas de corrente desenhado na Figura P9-53, onde os valores de estão em unidades de , e é a largura do duto para dentro da página. São mostrados os valores da função corrente nas paredes do duto. Qual é a porcentagem do escoamento que passa através da ramificação superior do duto?
Passo 1
A questão é sobre função corrente . Ela quer que a gente calcule, a partir dos valores de função corrente dados, a porcentagem de vazão volumétrica que passa pela ramificação de cima. Ou seja, o problema quer saber quanto vale a divisão da vazão pela vazão total que passa pelo duto.
onde a constante está multiplicando para converter a divisão em uma porcentagem.
Para fazer esse cálculo, o enunciado nos informa alguns dados que são mostrados na figura abaixo.
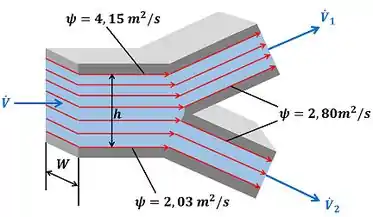
onde é a largura do duto, é a vazão volumétrica (vazão em volume) de fluido pela ramificação de baixo, é a altura do canal do duto e são os valores da função corrente em algumas linhas de corrente.
Agora que visualizamos os dados, podemos calcular o que queremos .
Passo 2
Temos que calcular , mas não sabemos quanto vale .
Para chegar no valor dessa divisão, temos primeiro que calcular a vazão volumétrica por unidade de largura que passa pela ramificação (de cima) e a vazão volumétrica total por unidade de largura . Para isso, usamos os valores informados de .
A equação 9-25 serve justamente para calcular a vazão volumétrica por unidade de largura de o escoamento que passa entre duas linhas de corrente com valores de conhecidos ( é o valor da linha de corrente de baixo e é o valor da linha de corrente de cima).
Por exemplo, a vazão total é a vazão que passa entre as linhas de corrente e . Com esses valores, chegamos no valor da vazão total por unidade de largura .
Já a vazão da ramificação de cima é a vazão que passa entre as linhas de corrente e . Com esses valores, chegamos no valor da vazão da ramificação de cima por unidade de largura .
Passo 3
Dividindo as duas vazões por unidade de largura que encontramos, chegamos em um valor de , porque é cancelado.
Substituindo esse resultado na equação de , achamos: