Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 15
Dada a instalação da figura, determinar a pressão para que a vazão seja 6 L/s. Em seguida, traçar a linha piezométrica e a linha de energia sobre a instalação, marcando o valor das respectivas alturas nas seções A, B, C, D, E, F e G. Dados: ; ; ; .
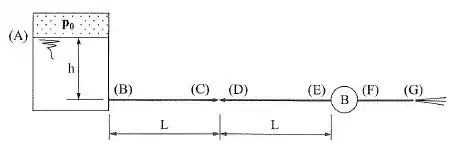
Passo 1
Tá legal, para descobrir o valor da pressão , vamos aplicar o equilíbrio de energia entre os pontos 0 e E:
Substituindo os valores conhecidos, ficamos com:
Nesse exercício, temos perda distribuída e localizada, então, a perda de carga pode ser escrita como:
Passo 2
Agora precisamos encontrar os valores para substituir na equação anterior. Vamos começar encontrando a velocidade do escoamento com o auxílio da equação para a vazão:
Então a perda de carga será:
Passo 3
Agora podemos retornar à equação para obtida no passo 1 e substituir os valores conhecidos:
Passo 4
Agora para encontrar o valor das linhas piezométricas dos pontos B até F, vamos aplicar o equilíbrio de energia entre os pontos adjacentes, então começando com os pontos 0 e B:
Substituindo os valores conhecidos:
E, para obter o valor da linha de energia, somamos a parcela da energia cinética, dada por , então, temos:
Agora para os pontos B e C:
Substituindo os valores conhecidos:
E, para obter o valor da linha de energia, somamos a parcela da energia cinética, dada por , então, temos:
Passo 5
Agora repetindo o processo para os pontos C e D:
Substituindo os valores conhecidos:
E, para obter o valor da linha de energia, somamos a parcela da energia cinética, dada por , então, temos:
Agora, antes de calcular o equilíbrio de energia entre os pontos E e F, precisamos descobrir o valor da carga da bomba, para isso, usando a fórmula da sua potência, temos:
Agora, aplicando o equilíbrio de energia entre os pontos E e F:
Substituindo os valores conhecidos:
E, para obter o valor da linha de energia, somamos a parcela da energia cinética, dada por , então, temos: