Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 14

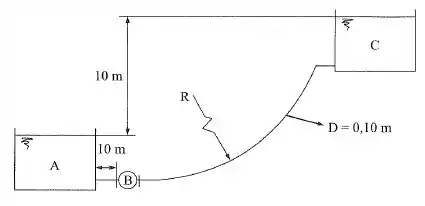
Na instalação da figura, um líquido de alta viscosidade cinemática ( ν = 10 - 4   m 2 / s ) , escoando laminarmente, é recalcado do reservatório A para C. O comprimento da tubulação, desde a saída da bomba B até a entrada do cotovelo, é 60 m, medidos ao longo do eixo do tubo. O raio R é muito grande e a distância entre a saída do cotovelo e a entrada do tanque C pode ser desprezada. Determinar:

a) a carga manométrica que a bomba deverá prover para obter-se uma vazão de 8 L/s;

b) a potência da bomba, cujo rendimento é de 70%.

Dados: k s (saída de A) = 0,78; γ = 8000   N / m 3 ; k s (cotovelo) = 0,6; k s (entrada de C) = 0,5.

Passo 1

Vamos começar esse exercício aplicando o equilíbrio de energia entre os pontos A e C:

H A + H B = H C + H p A , C

v A 2 2 g + p A γ + z A + H B = v C 2 2 g + p C γ + z C + H p A , C

Substituindo os valores conhecidos, ficamos com:

0 2 2 g + 0 γ + 0 + H B = 0 2 2 g + 0 + 10 + H p A , C → H B = 10 + H p A , C

Então, para encontrar a carga da bomba, e depois a sua potência, precisamos primeiro encontrar a perda de carga do sistema entre os pontos A e C. Nesse exercício, temos perda distribuída e localizada, então, a perda de carga pode ser escrita como:

H p A , C = f L v 2 2 g D H + v 2 2 g ∑ k s

Passo 2

Agora precisamos encontrar os valores para substituir na equação anterior. Vamos começar encontrando a velocidade do escoamento com o auxílio da equação para a vazão:

Q = v A → v = Q A = Q π D 2 4 = 8.10 - 3 π 0,1 2 4 → v = 1   m / s

Agora, vamos calcular o valor do número de Reynolds para o escoamento:

R e = v D ν = 1 0,1 10 - 4 → R e = 1000

Passo 3

Nesse caso, como o enunciado nos disse que temos um escoamento laminar, podemos usar a equação 7.11 apresentada nessa seção do livro para encontrar o valor de f , então, temos:

f = 64 R e = 64 1000 → f = 0,064

Então, substituindo os valores conhecidos na equação para a perda de carga do passo 1, temos:

H p A , C = f L v 2 2 g D H + v 2 2 g ∑ k s

H p A , C = 0,064 70 1 2 2 ( 10 ) ( 0,1 ) + 1 2 2 10 0,78 + 0,6 + 0,5 → H p A , C = 2,3   m

E, substituindo esse valor na equação para a carga da bomba encontrada no passo 1:

H B = 10 + H p A , C = 10 + 2,3 → H B = 12,3   m

Passo 4

Agora para letra b) basta aplicar a equação para a potência da bomba:

N B = γ Q H B η B = 8000 8.10 - 3 12,3 0,7 → N B = 1124,6   W

Resposta

H B = 12,3   m

N B = 1124,6   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um medicamento líquido, com a viscosidade e a massa específica da água, deve ser administrado através de uma agulha hipodérmica. O diâmetro interno da agulha é 0,25 mm e o seu comprimento é de 50 mm.
A Equação 8.23 dá o expoente, n , do perfil de velocidade de lei de potência como uma função do número de Reynolds na linha de centro, R e U , para escoamento turbulento completamente desenvolvido em
Para um escoamento pressurizado, em regime permanente e completamente desenvolvido de um fluido incompressível através de um canal retilíneo de comprimentoL , podemos definir a resistência hidráulica
Para a configuração de escoamento da Fig. 8.12, é sabido que a perda de carga é 1 m. Da entrada para a saída, a queda de pressão é 50 kPa, a velocidade dobra da entrada para a saída, e o aumento de el
Um tubo horizontal transporta fluido em escoamento turbulento completamente desenvolvido. A diferença de pressão estática medida entre duas seções é 35 kPa. A distância entre as seções é 10 m e o diâm