Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 85

Água escoa de um tubo horizontal para dentro de um grande tanque. O tubo está localizado a 2,5 m abaixo da superfície livre da água no tanque. A perda de carga é 2 kJ/kg. Calcule a velocidade média do escoamento no tubo.

Passo 1

Neste problema o objetivo é obter a velocidade média do escoamento em um tubo que se conecta a uma reservartório, conforme Figura abaixo.

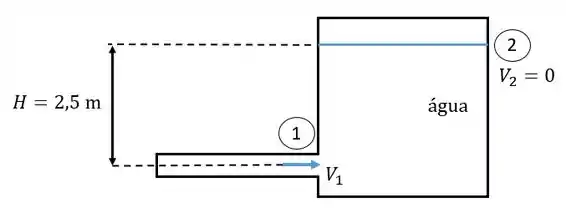
Para isso será utilizada a Equação de Energia, em kJ/kg, a ser aplicada entre as seções 1 e 2, conforme expressão:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l t

Para a aplicação da equação apresentada, as seguintes hipóteses são necessárias:

- regime permanente ( ∂ / ∂ t = 0 );

- escoamento incompressível ( ρ 1 = ρ 2 ,   ) e de água ( ρ = 1000   k g / m ³ );

- fator de correção α ≈ 1,0 em ambas as seções de avaliação (o problema não especificou tal parâmetro, logo adotaremos o valor de 1, o qual é característico de escoamento turbulento em tubos);

- p 1 = ρ g H ;

- p 2 = 0 (pressão atmosférica em termos manométrico);

- V 2 = 0 (é assumido reservatório com nível constante e, portanto, velocidade na seção 2 é nula);

- h l t = 2   k J / k g ;

- z 2 - z 1 = H = 2,5   m .

Passo 2

Utilizando a Equação de Energia e aplicando as hipósteses definidas no Passo 1:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l t

p 1 ρ + α V 1 2 2 + g z 1 = 0 + α × 0 + g z 2 + h l t

1 × V 1 2 2 = g ( z 2 - z 1 ) + h l t - p 1 ρ

Arranjando a expressão:

V 1 2 = 2 g ( z 2 - z 1 ) + 2 h l t - 2 p 1 ρ

Sabendo que z 2 - z 1 = H e p 1 = ρ g H :

V 1 2 = 2 g H + 2 h l t - 2 ρ g H ρ

V 1 2 = 2 g H + 2 h l t - 2 g H

V 1 2 = 2 h l t

Assim, a expressão da velocidade média do escoamento é dada por:

V 1 = 2 h l t

Passo 3

Calculando a velocidade V 1 :

V 1 = 2 h l t

V 1 = 2 × 2

Logo, a velocida média do escoamento ( V - = V 1 ) é de:

V - = 2   m / s

Resposta

V - = 2   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O ar entra em uma seção de 7m de comprimento de um duto retangular de seção transversal de 15c m× 20c m , feita de aço comercial, a 1a t m e 35 ° C , à velocidade média de 7m / s . Desprezando os efei
O perfil da velocidade no escoamento laminar completamente desenvolvido em um tubo circular de raio interno R = 2c m em m / s é dado por u r = 4 ( 1 - r 2 / R ² ) ² . Determine as velocidades média e
Considere o escoamento de óleo com ρ = 894k g / m 3 e μ = 2,33k g / m ∙ s em uma tubulação com 40c m de diâmetro a uma velocidade média de 0,5m / s . Uma seção de 300m de comprimento da tubulação pass
Repita p Problema 8 - 37 para o escoamento turbulento em tubos suaves para os quais o fator de atrito é dado por f = 0,184 R e - 2 . Qual seria a sua resposta para um escoamento totalmente turbulento
Amônia líquida a - 20 ° C escoa através de uma seção de 30m de comprimento de um tubo de cobre com 5m m de deâmetro a uma taxa de 0,15 k g / s . Determine a queda de pressão, a perda de carga e a potê