Os dados coletados pelo autor para o coeficiente de potência no PMR de 30 bombas diferentes são traçados em função da rotação específica na Figura P11.50. Determine se os valores de C*P para as três bombas do Problema P11.49 também se ajustam a essa correlação. Em caso afirmativo, proponha uma fórmula de ajuste de curva para os dados.

Pra começar a questão, temos que calcular a rotação especifica a partir da Equação 11.30b (página 784):

Depois, devemos calcular usando a Equação 11.23 (página 777)

Pra realizar esses cálculos, vamos precisar dos diâmetros e rotação das bombas dos três problemas já citados, além de suas vazões , alturas de carga e potências , todas nos seus pontos de máximo rendimento.

Embaixo eu vou mostrar uma tabela com todos os dados retirados dos respectivos problemas e os valores de e já calculados pra cada um deles:

Com os dados das tabelas, foi possível construir o gráfico abaixo, onde está demonstrada a correlação dos dados desse problema e destacados os pontos correspondentes ao ponto de máximo rendimento das bombas dos três problemas já citados:

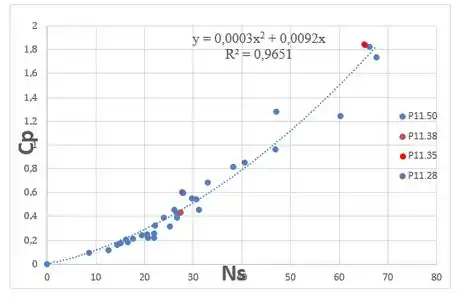
Como é possível ver, os dados das três bombas se ajustaram muito bem aos dados das outras 30 bombas, e o foi maior que , indicando forte correlação entre os dados.

Com esse gráfico foi possível fazer um ajuste de dados que resultou na equação , demonstrada no gráfico acima.

Pronto, matamos a questão juntos!