Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 3.Problemas - Ex. 49

Vapor d’água a uma temperatura de 250°C escoa através de uma tubulação de aço (AISI 1010) com diâmetro interno de 60 mm e diâmetro externo de 75 mm. O coeficiente convectivo entre o vapor e a superfície interna da tubulação é de 500   W / ( m 2 ⋅ K ) , enquanto aquele entre a superfície externa e a vizinhança é de 25   W / ( m 2 ⋅   K ) . A emissividade da tubulação é de 0,8 e a temperatura do ar e da vizinhança é de 20°C. Qual é a perda de calor por unidade de comprimento da tubulação?

Passo 1

Falaii galerinha do Responde ai, tudo belezinha?

  1. A temperatura do vapor é T ∞ , i = 523 K
  2. Os diâmetros interno e externo do tudo de aço são D i = 0.06 m   e   D o = 0.075   m
  3. Os coeficientes convectivos nas superfícies interna e externa do tudo são h i = 500   W / m 2 ⋅ K e h o = 25   W / m 2 ⋅ K
  4. A emissividade do tudo é ε = 0.8
  5. A temperatura do ar e do ambiente é T ∞ , o = T s u r = 293   K .

Precisamos determinar a perda de calor por unidade de comprimento do tudo, q ˙ = ?

O circuito térmico equivalente é mostrado adiante:

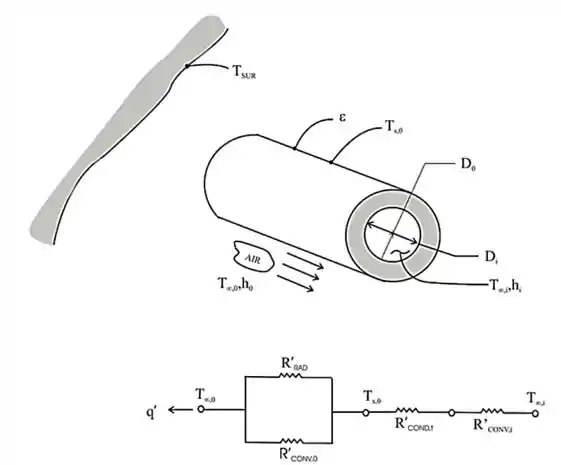
Passo 2

Ao realizar um balanço de energia na superfície externa, teremos

E i n = E o u t

Em conformidade

T ∞ , i - T S , o R c o n v , i + R c o n d , t = q c o n v , o + q r a d

A taxa de transferência de calor devido à convecção na superfície é expressa da seguinte maneira

q c o n v , o = π D o h o L ( T S , o - T ∞ , o )

A taxa de transferência de calor devido à radiação é expressa da seguinte maneira

q r a d = ε π D o L σ T S , o 4 - T s u r r 4

A resistência térmica devido à convecção na superfície interna é expressa como

R c o n v , i = 1 π D i L h i

A resistência térmica devido à condução da parede do tubo é expressa como

R c o n v   , t = ln ⁡ D o D i 2 π L k

Passo 3

Substituindo alguns dados numéricos nos parâmetros

q c o n v , o = π D o h o L ( T S , o - T ∞ , o )

= π × 0.075   m × 25   W / m 2 × K × L ( T S , o - 293 K )

= 5.89   L × ( T S , o - 293   K )

q r a d = ε π D o L σ T S , o 4 - T s u r r 4

= L 1.06876 × 10 - 8 T S , o 4 - 293 4

R c o n v , i = 1 π D i L h i

= 1 π × 0.06   m × L × 500   W / m 2 ⋅ K

= 0.01061 L   K / W

R c o n v   , t = ln ⁡ D o D i 2 π L k

= ln ⁡ 0.075 0.060 2 π L × 56.6   W / m ⋅ K

Passo 4

Vamos substituir agora todos os dados que temos, na seguinte formula

T ∞ , i - T S , o R c o n v , i + R c o n d , t = q c o n v , o + q r a d

523 - T S , o ( 0.01061 + 6.285 × 10 - 4 ) = 5.89 × T S , o - 293   K + 1.06876 × 10 - 8 T S , o 4 - 293 4

Ou

1.2 × 10 - 10 T S , o 4 + 1.06614 T S , o 4 - 543.2645 = 0

Passo 5

Vamos de tentativa e erro, para a solução da expressão a seguir

1.2 × 10 - 10 T S , o 4 + 1.06614 T S , o 4 - 543.2645 = 0

A perda de calor por unidade de comprimento do tubo de (1) é expressa da seguinte maneira

q ' = π D o h o L T S , o - T ∞ , o - ε π D o L σ T S , o 4 - T s u r r 4

q ' = π × 0.075 × 25 × K × 502.3 - 293 + 0.8 × 5.67 × K 4 × π × 0.075 502.3 4 - 293 4

q ' = 1834.466   W / m

“O coelho está certo, e ele é claramente o mais inteligente entre vocês!”

Resposta

Portanto, a perda de calor por unidade de comprimento do tudo é de 1834.466   W / m .

Exercícios de Livros Relacionados

29 - Água quente é transportada de uma estação de cogeração de potência para usuários comerciais e industriais através de tubos de aço com diâmetro D = 150m m . Cada tubo encontra-se no centro de um b
25 - Um pequeno dispositivo é usado para medir a temperatura superficial de um objeto. Uma junção de termopar, com diâmetroD=120μ m , está posicionada a uma distância z=100μ m da superfície de interes
22 - Uma janela de vidro duplo é constituída por duas folhas de vidro separadas por um espaço, com L = 0,2m m de espessura. Há vácuo neste espaço, o que elimina a condução e a convecção através dele.
34 - Seja o circuito integrado (chip) delgado do Problema 3.150. Ao invés de fixar o dissipador de calor à superfície do chip, um engenheiro sugere que um resfriamento suficiente poderia ser alcançado
23 - Um oleoduto, utilizado para o transporte de óleo cru, está enterrado no solo de modo que o seu eixo central se encontra a uma distância de 1,5m abaixo da superfície. O duto tem um diâmetro extern