Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 3.Problemas - Ex. 71

A distribuição de temperaturas, em regime estacionário, em uma parede plana composta por três materiais diferentes, todos com condutividade térmica constante, é mostrada a seguir

(a) Comente a respeito das magnitudes relativas de q 2 ' '   e   q 3 ' '   ,   e   d e   q 3 ' ' e   q 4 ' ' .

(b) Comente a respeito das magnitudes relativas de k A   e   k B ,   e   d e   k B   e   k C .

(c) Esboce o fluxo térmico como uma função de x.

Passo 1

Oii pessoal, show de bola??

“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”

Bora empurrar e macetar essa questãozinha comigo agora

  1. A distribuição de temperatura no estado estacionário em uma parada plana composta de três materiais é mostrada abaixo

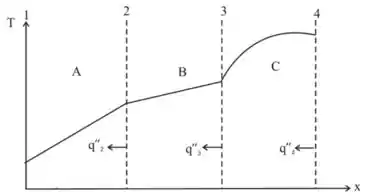
Vamos determinar

  1. Comentar as magnitudes relativas do fluxo de calor.
  2. Comentar as magnitudes relativas das condutividades térmicas.
  3. E pra finalizar vamos esboçar o gráfico da distribuição do fluxo de calor.

Passo 2

  1. A distribuição de temperatura é parabólica, portanto, mostra a existência de geração de calor. Como sabemos o fluxo de calor da lei de condução de Fourier

    2. q ' ' = k d T d x

    À medida de ‘y’ aumenta, o gradiente d T / d x diminui e, portanto, q ' ' também diminui.

    Por isso, q 4 ' ' < q 3 ' '

    Em A e B, a distribuição de temperatura é linear, o que garante que não haja geração de calor

    Por isso q 3 ' ' = q 2 ' ' .

    Passo 3

  2. Temos

    3. d T d x C > d T d x B

    k = - q ' ' d T / d x

    Portanto, como a condutividade térmica afeta inversamente q ' '

    k C < k B

    Temos também

    d T d x B < d T d x A

    k B > k A

    Passo 4

  3. A distribuição do fluxo de calor é mostrada a seguir

“Faça seus medos terem medo de você”

Resposta

Vide o passo a passo.

Exercícios de Livros Relacionados

O número de Knudsen, K n = λ I p m L , é um parâmetro adimensional usado para descrever efeitos potenciais em micro e nano escalas. Deduza uma expressão para a razão entre a resistência térmica devida
Um material nanolaminado é fabricado com um processo de deposição de camada atômica, que resulta em uma série de camadas alternadas empilhadas de tungstênio e óxido de alumínio, cada camada com δ = 0,
Ouro é comumente utilizado no empilhamento de semicondutores para formar interconexões que transportam sinais elétricos entre diferentes dispositivos no conjunto. Além de ser um bom condutor elétrico,
Módulos termoelétricos têm sido utilizados para gerar potência elétrica através do aproveitamento do calor gerado em fogões a lenha. Considere a instalação de um módulo termoelétrico do Exemplo 3.13 e
Um dos módulos termoelétricos do Problema 3.13 está instalado entre um gás quente a T ∞ ,1 = 450 ° C e um gás frio a T ∞ ,2 = 20 ° C . O coeficiente convectivo associado ao escoamento dos dois gases é