Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 31
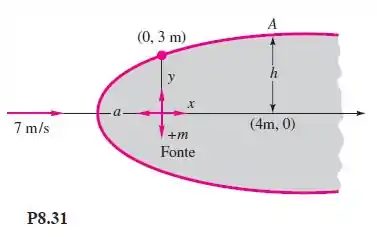
Um semicorpo de Rankine é formado como mostra a Figura P8.31. Para a velocidade da corrente e as dimensões do corpo mostradas, calcule (a) a intensidade da fonte m em m²/s, (b) a distância a, (c) a distância h e (d) a velocidade total no ponto A.
Passo 1
Bora pra mais uma!
A distância vertical acima da origem é um múltiplo conhecido de m e a:
A distância h é encontrada a partir da equação para a linha do corpo:
Em x=4m,
Então:
E:
Por fim, a velocidade resultante no ponto A é calculado pela equação 8.18:
Resposta
- .
Exercícios de Livros Relacionados
Em muitas ocasiões, precisamos transformar uma velocidade de coordenadas cartesianas ( x ,y ,z ) em coordenadas cilíndricas ( r ,θ ,z ) (ou vice-versa). Usando a Fig. P9–13 como guia, transforme os co
Usando a Fig. P9–13 como guia, transforme os componentes cartesianos de velocidade ( u ,v ,w ) em componentes cilíndricos de velocidade ( u r ,u θ ,u z ) . (Dica: Como o componente z da velocidade per
Um campo de velocidade permanente, bidimensional, incompressível, possui componentes de velocidade cartesiana u = C y x 2 +y 2 e v = - C x x 2 +y 2 , onde C é uma constante. Transforme essas component
A forma compressível da equação de continuidade é ∂ ρ ∂ t + ∇ →.ρ V → = 0 . Expanda essa equação o máximo possível nas coordenadas cartesianas ( x ,y ,z ) e ( u ,v ,w ) .
Verifique se o escoamento em espiral de linha de vórtices/sumidouros no plano r θ do Prob. 9–17 satisfaz a equação de continuidade incompressível bidimensional. O que acontece com a conservação de mas