Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 80

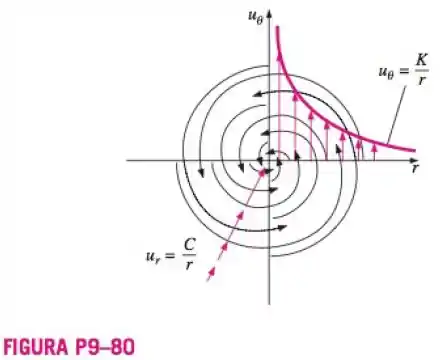
Considere o escoamento permanente, bidimensional, incompressível devido a um escoamento em espiral de linha de vórtices/sumidouros centrada no eixo z. Na Fig. P9-80 são mostradas linhas de corrente e vetores de velocidade. O campo de velocidade é u r = C r   e u θ = K r , onde C e K são constantes. Calcule a pressão em função de r   e   θ .

Passo 1

Shoooow galerinha, vamos continuando?!

O problema já nos disse que o escoamento é permanente e incompressível !!

Mas nós precisamos fazer algumas considerações, vamos assumir que o escoamento é completamente desenvolvido e que podemos negligenciar os efeitos da gravidade, g r = g θ = 0 .

Beleza !! Agora nós podemos começar lembrando da equação da continuidade para as coordenadas cilíndricas:

1 r ∂ r u r ∂ r + 1 r ∂ u θ ∂ θ = 0

As componentes da velocidade são dadas pelo problema, não é verdade?

u r = C r

u θ = K r

E agora? O que faremos?

Derivamos, certo?

∂ r u r ∂ r = ∂ ∂ r r × C r = 0

∂ u θ ∂ θ = ∂ ∂ θ K r = 0

Substituindo:

1 r ( 0 ) + 1 r ( 0 ) = 0

0 = 0

Isso nos diz que a equação da continuidade foi satisfeita!!

Passo 2

Se a equação da continuidade é satisfeita nós podemos usar a equação de Navier – Stokes.

Para a direção r e θ :

ρ ∂ u θ ∂ t + u r ∂ u θ ∂ r + u θ r ∂ u θ ∂ θ + u r u θ r = - 1 r ∂ P ∂ θ + ρ g θ + μ 1 r ∂ ∂ r r ∂ u θ ∂ r - u θ r 2 + 1 r 2 ∂ 2 u θ ∂ θ 2 - 2 r 2 ∂ u r ∂ θ

ρ ∂ u r ∂ t + u r ∂ u r ∂ r + u θ r ∂ u r ∂ θ - u θ 2 r = - ∂ P ∂ r + ρ g r + μ 1 r ∂ ∂ r r ∂ u r ∂ r - u r r 2 + 1 r 2 ∂ 2 u r ∂ θ 2 - 2 r 2 ∂ u θ ∂ θ

Então precisamos de algumas derivadas, certo? Para a direção r :

∂ u θ ∂ t = ∂ ∂ t K r = 0

∂ u θ ∂ r = ∂ ∂ r K r = - K r 2

∂ ∂ r r ∂ u θ ∂ r = ∂ ∂ r r × - K r 2 = ∂ ∂ r - K r = K r 2

∂ 2 u θ ∂ θ 2 = ∂ ∂ θ ∂ u θ ∂ θ = ∂ ∂ θ 0 = 0

∂ u r ∂ θ = ∂ ∂ θ C r = 0

Na direção θ :

∂ u r ∂ t = ∂ ∂ t C r = 0

∂ u r ∂ r = ∂ ∂ r C r = - C r 2

∂ u r ∂ θ = ∂ ∂ θ C r = 0

∂ ∂ r r ∂ u r ∂ r = ∂ ∂ r r × - C r 2 = ∂ ∂ r - C r = C r 2

∂ 2 u r ∂ θ 2 = ∂ ∂ θ ∂ u r ∂ θ = ∂ ∂ θ 0 = 0

E agora a gente substitui tudooo!!

Primeiro em θ :

ρ 0 + C r - K r 2 + K r r 0 + C r K r r = - 1 r ∂ P ∂ θ + ρ 0 + μ 1 r K r 2 - K r r 2 + 1 r 2 0 - 2 r 2 0

1 r ∂ P ∂ θ = μ K r 3 - K r 3 - ρ - C K r 3 + C K r 3

∂ P ∂ θ = 0

Então, a equação do momento para θ é satisfeita desde que possamos o campo de pressão satisfaça esta relação, ok?

Agora vamos para a direção r :

ρ 0 + C r - C r 2 + K r r 0 - K r 2 r = - ∂ P ∂ r + ρ 0 + μ 1 r C r 2 - C r r 2 + 1 r 2 0 - 2 r 2 0

∂ P ∂ r = μ C r 3 - C r 3 - ρ - C 2 r 3 - K 2 r 3

∂ P ∂ r = ρ C 2 + K 2 r 3

Da mesma forma que a anterior, a equação do momento para r é satisfeita desde que possamos o campo de pressão satisfaça esta relação !!

Passo 3

Nós percebemos que para duas dimensões, a pressão deve ser dada em função de r e de θ , não é?

Então, para que nós possamos calcular a pressão seja uma função regular de r e θ um requisito é essencial !!

Matematicamente, a derivada cruzada da pressão deve ser igual, ok?

Ou seja:

∂ 2 P ∂ r ∂ θ = ∂ 2 P ∂ θ ∂ r

Calculemos então cada um separadamente:

∂ 2 P ∂ r ∂ θ = ∂ ∂ r ∂ P ∂ θ = ∂ ∂ r 0 = 0

∂ 2 P ∂ θ ∂ r = ∂ ∂ θ ∂ P ∂ r = ∂ ∂ θ ρ C 2 + K 2 r 3 = 0

Então:

∂ 2 P ∂ r ∂ θ = ∂ 2 P ∂ θ ∂ r

Como as derivadas cruzadas não são iguais, a pressão é uma função regular!!

Agora é só calcular!!

Passo 4

Boom galerinha, para obter a pressão nós podemos usar uma as equações das derivadas que nós acabamos de achar no Passo 2e integrá-las !

Vamos começar pela equação do momento para θ :

∫ ∂ P ∂ θ = ∫ 0

∫ ∂ P = ∫ 0 . ∂ θ

P r , θ = 0 + g ( r )

Porque adicionamos esta função de r ?

Neste caso g ( r ) é a nossa constante, já que aqui temos uma derivada parcial quando derivarmos g ( r ) ela resultará zeroo!!

Muito importante isso, porque agora a pressão será:

P r , θ = g ( r )

Se derivarmos em relação a r :

∂ P ∂ r = g ' ( r )

Substituindo ∂ P ∂ r :

g ' r = ρ C 2 + K 2 r 3

Para acharmos a pressão precisamos de g r , então vãos integrar esta equação, ok?

∫ g ' r . d r = ∫ ρ C 2 + K 2 r 3 . d r

g r = ρ C 2 + K 2 ∫ r - 3 . d r

g r = ρ C 2 + K 2 . r - 2 - 2 + C 1

g r = - ρ C 2 + K 2 2 r 2 + C 1

Portanto:

P r , θ = g ( r ) = - ρ C 2 + K 2 2 r 2 + C 1

Legaal, não foi ?!

Resposta

P r , θ = - ρ C 2 + K 2 2 r 2 + C 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

59 – Considere o escoamento não viscoso em torno de um cilindro com circulação nula, como na Fig. 8.14a (mostrada abaixo). Encontre (a) o ponto sobre a superfície frontal onde a aceleração do fluido a
PP8.3 – Considere água a 20°C escoando a 12 m/s em um canal. Um oval de Rankine cilíndrica de 40 cm de comprimento é posicionada paralelamente ao escoamento, onde a pressão estática da água é 120 kPa.
PP8.2 – Modifique o Problema PP8.1 para determinar a distribuição de fontes pontuais que aproxima um corpo de revolução de formato “0018”. Uma vez que não existe resultados publicados, simplesmente se
An incompressible, irrotational, two-dimensional fl ow hasthe following stream function in polar coordinates:ψ 5 A rn sin (nθ) where A and n are constants.Find an expression for the velocity potential
Consider the function f 5 ay 2 by3. (a) Could this represent a realistic velocity potential? Extra credit: (b) Could itrepresent a stream function?