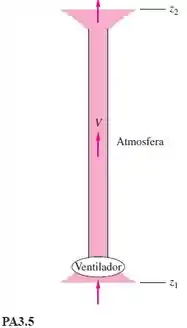
Desprezar o atrito às vezes pode levar a resultados estranhos. Alguém lhe pediu para analisar e discutir o seguinte exemplo na Figura . Um ventilador sopra ar através de um duto da seção para a seção , como mostra a figura. Admita que a massa específica do ar é constante. Desprezando as perdas por atrito, encontre uma relação entre a altura de energia do ventilador e a vazão e a variação de elevação. Depois explique o que pode ser um resultado inesperado.

E aí, tudo bem? Bora matar essa questão comigo!

Essa vamos matar rapidinho, se negarmos o atrito, para a equação de Bernoulli , assim:

Como estamos exaurindo ar da atmosfera e jogando na atmosfera, temos que:

Assim:

A altura de energia , isso pode ser explicado devido ao peso do ar, como seu peso é praticamente insignificante se comparado à fluidos como água, sem o atrito, a “potência” necessária para empurrar o ar é desprezivel!

Isso é tudo pessoal, conseguimos mais uma! \o/