Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 109

Um motor-foguete a 7000 m de altitude consome 45 kg/s de ar e adiciona 550 kJ/kg na câmara de combustão. A seção transversal da câmara é de 0,5 m², e o ar entra na câmara a 80 kPa e 5°C. Após a combustão o ar se expande através de um bocal convergente isentrópico até a saída à pressão atmosférica. Calcule (a) o diâmetro da garganta do bocal, (b) a velocidade de saída no bocal e (c) o empuxo produzido pelo motor.

Passo 1

Bem, primeiramente como você está?! Espero que esteja tudo tranquilo por aí pra gente seguir para mais um desafio da mecflu e termodinâmica aplicada

Antes de mais nada bora desenhar hehehe

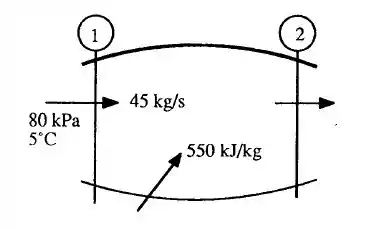
Passo 2

Na tabela A.6 do finalzinho do livro, você vai ver que na altitude de 7000 m, temos que a pressão p a = 41043   P a e T a = 242,66   K . Então essas serão as condições na saída do nosso sistema desenhado ali em cima, beleza?

Vamos agora calcular então o número de Mach!!

M a = V a = V k R T

Bem, agora na tabela A.2 você vai perceber que pro ar temos que o valor de k = 1,4 e R = 287 m²/s².K (Note que estamos considerando ar seco, uma vez que a questão não disse nada sobre a umidade do ar). Lembre-se que a temperatura na câmara de combustão é de 5°C, ou seja, 278 K.

Vamos lembrar quem é nosso valor de velocidade!!

m ˙ = ρ A V = 45 k g s

Mas como calculamos a densidade desse cara? Considerando um gás ideal, temos que:

ρ 1 = p 1 R T 1 = 80000 287 278 = 1   k g / m ³

45 = 1 0,5 V 1 → V 1 = 90   m / s

M a = 90 1,4 287 278 = 0,27

Com esse valor, a gente pode ir na tabela B.4 do livro e observar que T o 1 T o * = 0,29

Além disso, podemos calcular quem será nossa T o 1 = T + V 2 2 C P = 2 78 + 90 2 2 1005 = 282   K

Portanto T o * = 282 0,29 = 973   K

Passo 3

Com a adição de calor, temos que T o 2 = T o 1 + q a d d C P = 282 + 550000 1005 = 829   K

Portanto, T o 2 T o * = 829 973 = 0,85

Com esse valor podemos ler a tabela B.4 o valor de M a 2 = 0,63 . Também ainda nessa mesma tabela, a gente vai ler que p 1 p * = 2,18   e p 2 p * = 1,54

p 2 = 1,54 p *

p * = p 1 2,18

p 2 = 1,54 p 1 2,18 = 1,54   80 2,18 = 57   k P a

Portanto, p o 2 = p 2 1 + 0,2 M a 2 2 3,5 = 57 1 + 0,2 0,63 2 3,5 = 74   k P a

Passo 4

(b) Com os dados conhecidos da seção 2 do nosso problema, podemos expandir isentropicamente para atmosfera:

p s a i d a p o 2 = 41043 57000 = 0,72 = 1 + 0,2 M a s a í d a 2 3,5 → M a s a í d a = 0,7

Com isso, podemos calcular T s a í d a T o 2 = T s a í d a 829 = 0,910

Aí você vai me perguntar, mas de onde saiu esse valor de 0,910?? Então, também da tabela B.4 do livro, pois uma vez que conhecemos o valo de Ma, podemos olhar lá e observar a relação entre as temperaturas e pressões, beleza?

T s a í d a = 775   K

ρ s a í d a = p s a í d a R T s a í d a = 41043 287 775 = 0,189   k g / m ³

Podemos também calcular o valor da velocidade do som, a s a í d a = k R T s a í d a = 551   m / s

M a s a í d a = V s a í d a a s a í d a → V s a í d a = 0,7 551 = 385   m / s

Passo 5

(a) e (c) Agora que a gente conhece a velocidade de saída, é beleza calcular o diâmetro também de saída, porque podemos fazer uma relação com a vazão mássica!!!

m ˙ = ρ s a í d a A s a í d a V s a í d a = ρ s a í d a π 4 D 2 V s a í d a

m ˙ = 0,189 π 4 D 2 385 = 45 k g s

D = 0,89   m

E agora fica tranquilão de calcularmos o empuxo, pois ele será dado pela equação:

F e m p u x o = m ˙ V s a í d a = 45 385 = 17300   N

Resposta

a D = 0,89   m

b V s a í d a = 385 m s

c F e m p u x o = 17,3   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoa, com baixa velocidade, através de um tubo circular com diâmetro interno de 50 mm. Um tampão arredondado e liso, de 38 mm de diâmetro, é mantido na extremidade do tubo onde a água é descarre
Ar a alta pressão força uma corrente de água através de um pequeno orifício arredondado, de área A, em um tanque. A pressão do ar é suficientemente grande para que a gravidade possa ser desprezada. O
Repita o Problema 6.81, considerando que o ar se expande de forma tão rápida que a expansão pode ser considerada como adiabática.
Descreva a distribuição de pressões sobre o exterior de um edifício de lojas sujeito a um vento em regime permanente. Identifique os locais de pressões máxima e mínima sobre o lado externo do prédio.
Um aspirador produz sucção por meio de uma corrente de água escoando através de um venturi. Analise a forma e as dimensões de tal aparelho. Comente sobre as limitações sobre o seu uso.