Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 43
Determinar a altura do óleo para que o corpo () passe da posição para a posição .
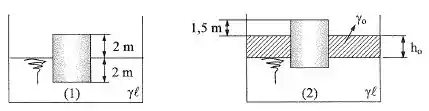
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Analisando o primeiro momento podemos descobrir o peso específico do líquido . Temos que o empuxo é igual ao peso do corpo. Logo:
Como o volume submerso é metade do volume do corpo, temos que:
Portanto:
Passo 2
Agora analisando a segunda situação, como temos dois líquidos agindo sobre o corpo, teremos também dois empuxos. A condição de equilíbrio é dada por:
O volume do cilindro é igual ao produto da área da base pela altura, portanto:
Como a altura submersa do líquido é dada por:
Portanto:
Substituindo os valores temos que:
Resposta
Exercícios de Livros Relacionados
A lata na Figura P2.104 flutua na posição mostrada. Qual é seu peso em N?
Diz-se que Arquimedes descobriu as leis do empuxo quando questionado pelo rei Hierão de Siracusa para determinar se sua nova coroa era de ouro puro (d = 19,3). Arquimedes pesou a coroa no ar e achou 1
Um balão esférico com hélio tem 2,5 m de diâmetro e uma massa total de 6,7 kg. Quando ele é solto na atmosfera padrão dos Estados Unidos, a que altitude ele irá estabilizar-se?
Uma bola sólida de alumínio (d = 2,7) com 7 cm de diâmetro e uma bola sólida de latão (d = 8,5) se equilibram perfeitamente quando submersas em um líquido, como mostra a Figura P2.108. (a) Se o fluido
Um densímetro flutua em um nível que é uma medida da densidade do líquido. A haste é de diâmetro constante D e o peso no fundo estabiliza o corpo para flutuar verticalmente, como mostra a Figura P2.10