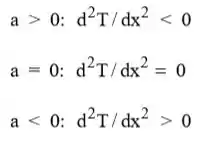Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 8
Para determinar o efeito da dependência da condutividade térmica em relação à temperatura na distribuição de temperaturas em um sólido, considere um material para o qual essa dependência possa ser representada por
na qual é uma constante positiva e a é um coeficiente que pode ser positivo ou negativo. Esboce a distribuição de temperaturas, em regime estacionário, associada à transferência de calor através de uma parede plana para os três casos: e.
Passo 1
Beleza galerinha, vamos lá! Da lei de Fourier e da forma de ,
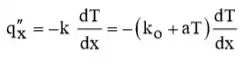
Passo 2
A forma da distribuição da temperatura pode ser inferida a partir do conhecimento de Uma vez que é independente de para as condições prescritas,
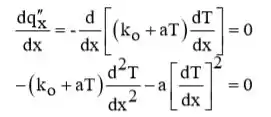
Logo,
Onde,
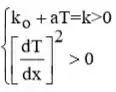
Passo 3
Isso se segue que:
Resposta
Exercícios de Livros Relacionados
29 – A partir do balanço de energia do elemento de volume, derive a equação de condução de calor bidimensional transiente em coordenadas retangulares para T ( x , y , t ) , com condutividade térmica c
30 – A partir do balanço de energia do elemento de volume em forma de anel, derive a equação de condução de calor bidimensional permanente em coordenadas cilíndricas para T ( r , z ) , com condutivida
51 – Considere um bastão sólido de formato cilíndrico cuja superfície lateral é mantida a uma temperatura constante, enquanto as extremidades da superfície são perfeitamente isoladas. A condutividade
53 – Considere um bastão sólido de formato cilíndrico cujas extremidades são mantidas a temperaturas constantes isolada. Não há geração de calor. Podemos afirmar que a temperatura ao longo do eixo do
38 – Por que tentamos evitar condições de contorno de radiação em análise de transferência de calor?