Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 96
Uma casca cilíndrica com raios interno e externo e , respectivamente, é feita com um material gerador de calor que fornece uma taxa volumétrica de geração uniforme (W/m³) de . A superfície interna é isolada, enquanto a superfície externa da casca está exposta a uma fluido à com um coeficiente convectivo h.
(a) Obtenha uma expressão para a distribuição de temperaturas em estado estacionário, T(r), na casca, representando o seu resultado em termos de , , , h, e da condutividade térmica k do material da casca.
(b) Determine uma expressão para a taxa de transferência de calor, , no raio externo da casca, em termos de e das dimensões da casca.
Passo 1
Beleza! A primeira coisa que vamos fazer é ilustrar o problema, então, teremos:
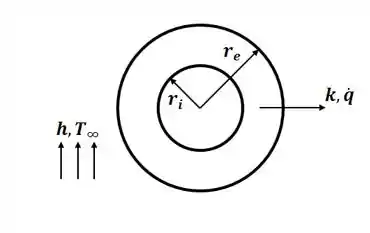
Agora, diante do problema, sabemos que a equação geral para a distribuição de temperatura será:
Agora, precisamos encontrar o valor das constantes e . Como sabemos que a superfície interna, em é isolada, temos:
Então, substituindo esses valores na derivada da equação da temperatura, temos:
Passo 2
Agora, para encontrar nós vamos usar a condição na extremidade , onde sabemos que a transferência de calor por condução é igual à por convecção, então, temos:
Substituindo as expressões conhecidas, temos:
Isolando dessa expressão, chegamos em:
Dessa forma, o perfil de temperatura será:
Passo 3
Agora, para a letra (b), para encontrar a taxa de transferência de calor vamos aplicar um balanço de energia na casca, então, teremos que a taxa de energia gerada será a taxa de calor . Então, temos:
E a taxa de energia gerada pode ser escrita como:
Então, a equação acima se torna: