Considere condução de calor unidimensional, em regime estacionário, através da geometria axissimétrica mostrada na figura.

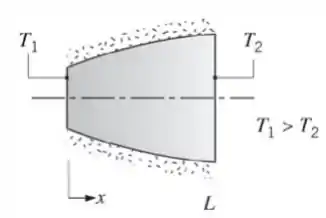
Supondo propriedades constantes e ausência de geração interna de calor, esboce a distribuição de temperaturas em um sistema de coordenadas . Explique sucintamente a forma da curva proposta.

Isso por causa da simetria no eixo ! E que . Ou seja, a taxa de calor dentro do objeto é constante em todo o lado. Da lei de Fourier,

E como e são ambos constantes, segue-se que,

Ou seja, o produto da área da secção transversal normal à taxa de calor e ao gradiente de temperatura permanece constante e independente da distância . Segue-se que como o eixo aumenta com , então deve diminuir com o aumento de . Assim, a distribuição da temperatura aparece como mostrado acima.