30 – A partir do balanço de energia do elemento de volume em forma de anel, derive a equação de condução de calor bidimensional permanente em coordenadas cilíndricas para , com condutividade térmica constante e sem geração de calor.
Passo 1
Desenhe o diagrama esquemático do elemento de volume em forma de anel.
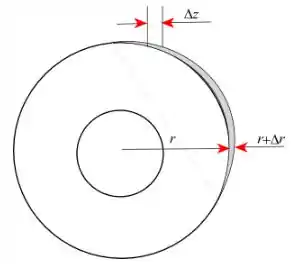
Passo 2
Considere um elemento de volume fino em forma de anel, de largura z e espessura r em um cilindro. Escreva a equação do balanço de energia no elemento anelar por um pequeno intervalo no estado estacionário e sem geração de calor com o sistema bidimensional.
Onde:
é a energia térmica em r
é a energia térmica em z
é a energia térmica em
é a energia térmica em
é a energia térmica total adquirida pelo elemento
A mudança de energia no elemento pode ser expressa como,
Sabemos que:
Logo,
Passo 3
Substituindo na fórmula temos,
Divida a equação por , temos:
Passo 4
A partir da definição da derivada e da lei de Fourier de condução de calor, temos:
Juntando as equações, temos:
Uma vez que o material possui condutividade térmica constante.
a difusividade térmica do material é. Logo,
Como estamos trabalhando em um estado estacionário .
Assim, a equação bidimensional de condução de calor em estado estacionário em coordenadas cilíndricas para o anel sem geração de calor é