Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 89
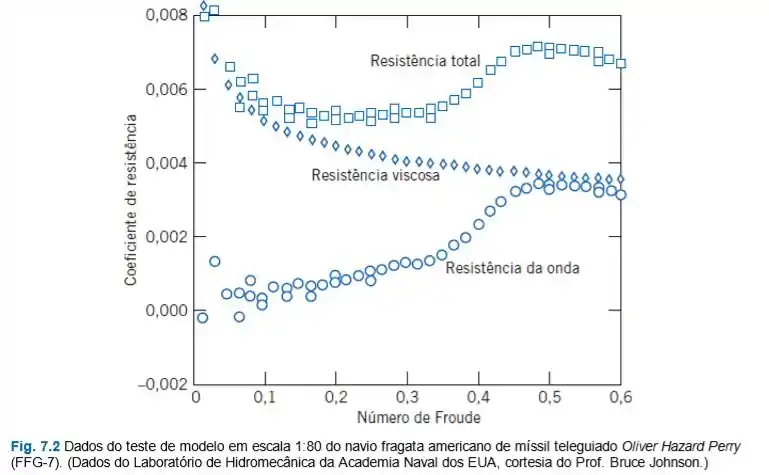
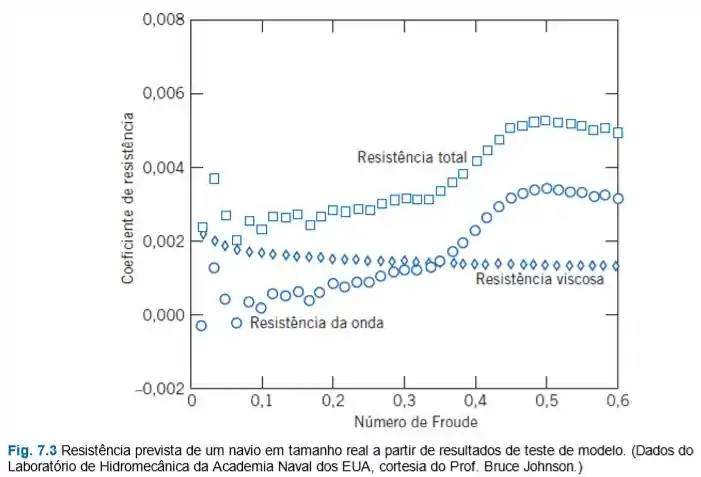
Na Seção 7.6, a resistência de onda e a resitência viscosa sobre um modelo e sobre um protótipo de navio foram discutidas. Para o protótipo, e . A partir dos dados das Figs. 7.2 e 7.3, trace um gráfico das resistências (em ) total, viscosa e de onda experimentadas pelo protótipo, como uma função da velocidade. Trace um gráfico similar para o modelo. Discuta os resultados. Finalmente, plote a potência requerida para o navio protótipo superar a resitência total.
Passo 1
Listinha do que a gente precisa fazer:
- traçar um gráfico das resistências (em ) total, viscosa e de onda experimentadas pelo protótipo, como uma função da velocidade
- traçar um gráfico das resistências (em ) total, viscosa e de onda experimentadas pelo modelo, como uma função da velocidade
- plotar a potência requerida para o navio protótipo superar a resitência total
Informações importantes:
- comprimento:
- área:
- escala
- água do mar a : ,
Vamos começar!
Passo 2
Temos um gráfico que relaciona os coeficientes de resistência aos números de Froude. Como a gente pode usar isso?
Temos que:
Ih achamos uma relação entre e a variável do nosso gráfico.
E podemos usar essa relação aqui:
Para achar as resistências (todas as 3), porque já temos os .
Logo, podemos montar um gráfico: , sendo função de também pelo gráfico.
Passo 3
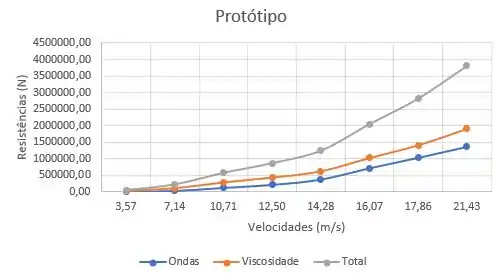
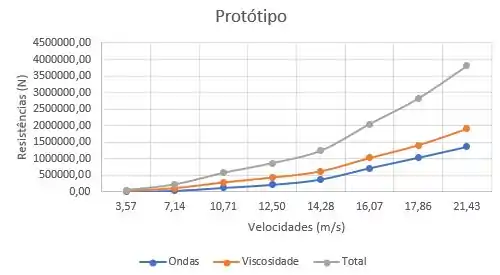
Usando ponto a ponto do gráfico do protótipo e substituindo os dados do enunciado nessas duas equações, ficamos com esse gráfico para o protótipo:
Passo 4
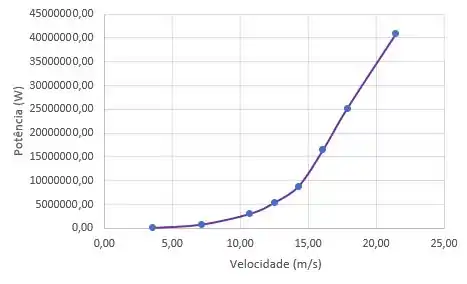
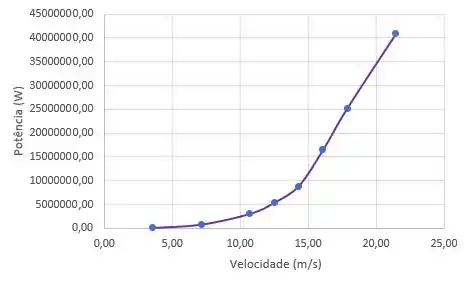
Para potência a gente usa:
Passo 5
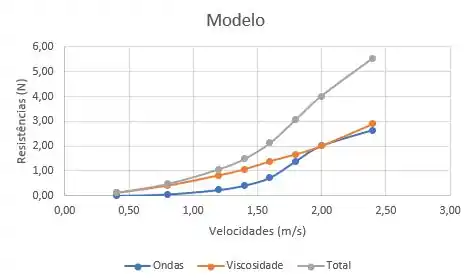
Usando ponto a ponto do gráfico do modelo e substituindo os dados do enunciado nessas duas equações (lembrando de usar a escala), ficamos com esse gráfico para o modelo:
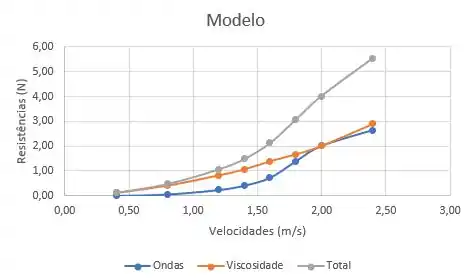
Fazendo umas observações sobre os gráficos, vemos que a viscosidade é a resistência dominante em velocidades baixas. Outro ponto é que para o modelo, as resistências de onda são muito mais signicantes em velocidades altas.
Resposta
