Quando um peso de 22 N é colocado na extremidade de uma barra de madeira flutuante na Figura P2.119, a barra inclina a um ângulo theta com seu canto superior direito na superfície, como mostra a figura. Determine (a) o ângulo theta e (b) a densidade da madeira. (Dica: As forças verticais e os momentos em relação ao centroide da barra devem estar equilibrados.)
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.8 do livro, chamada “Empuxo; princípios de Arquimedes”.
Nesse problema, como mostra a figura que ilustra a questão, temos uma barra de madeira de de comprimento e de base . Além disso, temos um peso de em uma de sua extremidades, fazendo com que a barra incline num ângulo .
O enunciado pede que a gente calcule o ângulo da barra e também a densidade da madeira. Pra isso, vamos dar uma olhada nesse esquema de forças na figura abaixo:
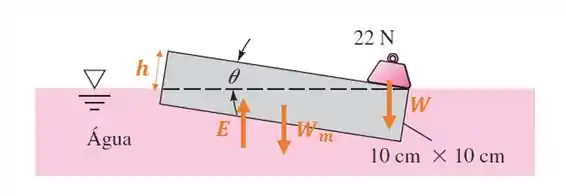
Sendo: o empuxo; o peso da madeira; e o peso colocado na extremidade da barra.
Com base nisso, nos próximos passos vou te mostrar como calcular essas forças e fazer um balanço de forças e de momentos para calcular o ângulo e a densidade .
Vem comigo pra resolver a questão!

Passo 2
Pra começo de conversa, vamos o esquema lá em cima. Temos uma altura da parte emersa da barra, que forma um triângulo. Utilizando relações trigonométricas, podemos defini-la .
Deixando isso claro, vamos calcular agora as forças.
A primeira delas é o empuxo . O empuxo pode ser calculado a partir do produto do peso específico da água e do volume da barra submerso. Esse volume submerso vai ser, então, o volume total da barra menos o volume emerso, que é um triângulo:
A linha de ação dessas forças com relação ao peso será de para o empuxo se considerar toda a barra e para a área emersa, que é um triângulo.
O peso da madeira pode ser calculada a partir da equação:
E a linha de ação até o peso é .
E, por fim, a linha de ação da força peso com relação a ela mesma é nula.
Passo 3
Agora, pra finalizar a questão, iremos calcular os valores de , e com ele o valor de , e de .
O balanço de forças, que deve ser nulo, é igual a:
Da mesma maneira, o balanço de momento que também deve ser nulo:
Agora, podemos combinar as duas equações pra achar e :
Com podemos achar :
Pronto, matamos a questão juntos!

Resposta
(a) O ângulo no qual a barra se inclina é
(b) A densidade da madeira da barra é