Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 103
Uma esfera de raio R está parcialmente imersa, a uma profundidade d, em um líquido com densidade relativa SG. Obtenha uma expressão algébrica para a força de empuxo atuando sobre a esfera como uma função da profundidade de submersão . Plote os
resultados para um faixa de profundidade na água de .
Passo 1
Temos nesse problema uma esfera parcialmente imersa em um líquido de gravidade específica . Devemos encontrar uma expressão algébrica para a força de empuxo e plotar um gráfico de resultados.
Para isso, fazemos algumas considerações: fluido estático e incompressível; pressão atmosférica atuando em todos os lugares.
Aplicaremos a seguinte equação hidrostática:
(a força de empuxo é igual ao peso do fluido deslocado)
Passo 2
Começamos pelo diagrama de corpo livre:
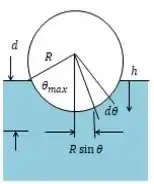
Temos:
Assim, precisamos de uma expressão para o volume deslocado de fluido em um , em que a profundidade é .
Então, se queremos encontrar o volume da parte submersa da esfera, calculamos:
Mas, como o , nós temos:
Assim, a força flutuante será:
Passo 3
Portanto, o gráfico de resultados para um faixa de profundidade na água de , fica da seguinte forma:
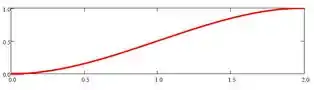
Prontinho!!