Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 24

Determine a pressão manométrica em kPa no ponto a, se o líquido A tiver densidade relativa 1,20 e o líquido B tiver 0,75. O líquido em torno do ponto a é água e o tanque da esquerda está aberto para a atmosfera.

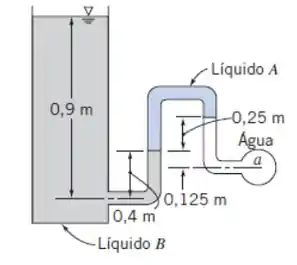
Passo 1

Bora achar a pressão manométrica do ponto a!!

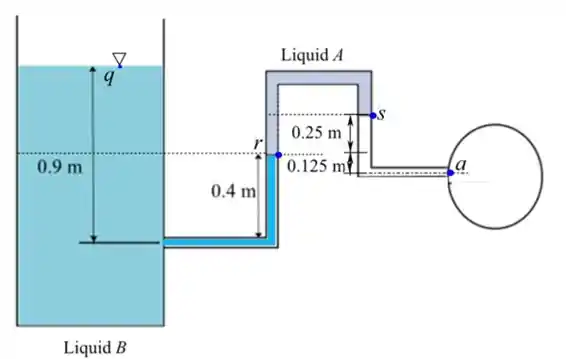
Pra começar, vamos fazer um esqueminha definindo os pontos que podem ser interessantes pra a gente.

Mas como eu sei quais pontos são interessantes! É só marcar as superfícies livres e também as interfaces!!

Usaremos a seguinte fórmula para determinar a diferença de pressão entre dois pontos diferentes da mesma coluna de líquido:

P a - P b = ρ g h a b

Passo 2

Vamos escrever a diferença de pressão entre o ponto q e r

P r - P q = ρ B g h q r

P r - P a t m = ρ B g × ( 0.9 - 0.4 )

P r - P a t m = 0.5 ρ B g                   ( 1 )

Vamos identificar que a pressão no ponto q se torna igual à pressão atmosférica.

Escrevendo a diferença de pressão entre o ponto r e s

P s - P r = - ρ A g h r s

= - ρ A g × 0.25          

= - 0.25 ρ A g         ( 2 )

Vamos escrever a diferença de pressão entre o ponto s e a

P a - P s = ρ H 2 O g h s a

= ρ H 2 O g × 0.25 + 0.125

= 0.375 ρ H 2 O g                 ( 3 )

Passo 3

Adicionando as equações (1), (2), (3)

P r - P a t m + P s - P r + P a - P s = 0.5 ρ B g - 0.25 ρ A g + 0.375 ρ H 2 O g  

P a = 0.5 ρ B g - 0.25 ρ A g + 0.375 ρ H 2 O g + P a t m

P a = g 0.5 ρ B - 0.25 ρ A + 0.375 ρ H 2 O + P a t m           ( 4 )

Passo 4

Vamos expressar as densidades do líquido A e do líquido B em termos de densidade da água e suas respectivas densidades individuais

P a = g 0.5 ρ B - 0.25 ρ A + 0.375 ρ H 2 O + P a t m

P a = 0.5 S G × ρ H 2 O - 0.25 S G A × ρ H 2 O + 0.375 ρ H 2 O + P a t m           ( 5 )

O b s e r v a ç õ e s  

  • Pressão manométrica significa a pressão medida tomando a atmostera local como ponto de referência
  • Ponto de referência é o ponto a partir do qual se deve iniciar a contagem. Portanto, neste caso, a pressão atmosférica é o ponto de referência. Entretanto, não devemos contar a mesma.

Passo 5

Entretanto, removemdo o termo P a t m da equação (5), e substituindo o P a m a n o m é t r i c a por P a na equação (5), teremos:

P a m a n o m é t r i c a   = 0.5 S G × ρ H 2 O - 0.25 S G A × ρ H 2 O + 0.375 ρ H 2 O + P a t m           ( 5 )

Substituindo os valores

= 9.81 0.5 0.75 × 1000 - 0.25 1.20 × 1000 + 0.375 × 1000

P a m a n o m é t r i c a = 4414.5   N / m 2

P a m a n o m é t r i c a = 4414.5 N m 2 × 1 k N / m 2 10 3   N / m 2

P a m a n o m é t r i c a = 4.4145   k N / m 2

O b s =   k N / m 2 = k P a

Resposta

P a m a n o m é t r i c a = 4.4145   k N / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um manômetro de fluido duplo preso a um tubo de ar mostrado na Figura P3-40. Se a gravidade específica de um fluido for 13,55, determine a gravidade específica do outro fluido para a pressão
Considere o sistema mostrado na Figura P3 – 42. Se uma alteração de 0,7k P a na pressão do ar fizer com que a interface entre a água salgada e o mercúrio da coluna da direita caia em 5m m no nível da
A diferença de pressão entre um tubo de óleo e um tubo de água é medida por um manômetro de fluido duplo, como mostra a Figura P3 – 41. Para as alturas de fluido e gravidades especificas dadas, calcul
Duas câmaras com o mesmo fluido na base estão separadas por um pistão com peso 25 N, como mostra a Figura P3-39. Calcule as pressões manométricas das câmaras A e B.
Os dois tanques de água estão conectados entre si através de um manômetro de mercúrio com tubos inclinados, como mostra a Figura P3-43. Se a diferença de pressão entre os dois tanques for de 20k P a ,