Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 43

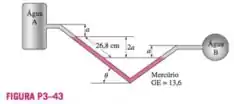
Os dois tanques de água estão conectados entre si através de um manômetro de mercúrio com tubos inclinados, como mostra a Figura P3-43. Se a diferença de pressão entre os dois tanques for de 20   k P a , calcule a e θ .

Passo 1

Temos que a gravidade específica do mercúrio é de 13,6 e iremos considerar que a densidade padrão da água é ρ w   =   1000   k g / m 3 .

Começando com a pressão no tanque A e movendo-se ao longo do tubo, adicionando (à medida que descemos) ou subtraindo (à medida que subimos) os termos ρ g h até chegarmos ao tanque B.

Definindo o resultado igual a P B , teremos a seguinte formulação:

P A + ρ w g a + ρ H g g 2 a - ρ w g a = P B

2 ρ H g g a = P B - P A

Passo 2

Muito bem!! Agora podemos reorganizar e substituir os valores conhecidos, ou seja...

a = P B - P A 2 ρ H g g = 20 k N m 2 2 13,6 1000 k g m 3 9,81 m s 2 1000 k g ∙ m s 2 1   k N

a = 0,0750   m = 7,50   c m

Passo 3

Por considerações geométricas, temos a seguinte relação:

26,8 sen ⁡ θ = 2 a

Portanto,

sen ⁡ θ = 2 a 26,8 = 2 × 7,50 26,8 = 0,560

θ = 34,0 °

Resposta

Portanto os valores de a e θ , são respectivamente:

a = 7,50   c m

θ = 34,0 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um experimento simples há muito tempo é usado para demonstrar como a pressão negativa evita que a água seja derramada para fora de um copo invertido. Um copo completamente cheio com água e coberto com
Considere um manômetro de fluido duplo preso a um tubo de ar mostrado na Figura P3-40. Se a gravidade específica de um fluido for 13,55, determine a gravidade específica do outro fluido para a pressão
Considere o sistema mostrado na Figura P3 – 42. Se uma alteração de 0,7k P a na pressão do ar fizer com que a interface entre a água salgada e o mercúrio da coluna da direita caia em 5m m no nível da
A diferença de pressão entre um tubo de óleo e um tubo de água é medida por um manômetro de fluido duplo, como mostra a Figura P3 – 41. Para as alturas de fluido e gravidades especificas dadas, calcul
Duas câmaras com o mesmo fluido na base estão separadas por um pistão com peso 25 N, como mostra a Figura P3-39. Calcule as pressões manométricas das câmaras A e B.