Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 111

Devido à sua comparativamente alta condutividade térmica, a água é um fluido com preferência para o resfriamento convectivo. Entretanto, em aplicações envolvendo dispositivos eletrônicos, a água não pode entrar em contato com esses dispositivos, que têm que ser então hermeticamente selados. Para evitar complexidades de projeto e operacionais e para garantir que os dispositivos não sejam deixados inoperantes pelo contato com o refrigerante, um fluido dielétrico é normalmente usado no lugar da água. Muitos gases têm excelentes características dielétricas e, apesar de suas pobres propriedades em relação à transferência de calor, o ar é a escolha comum para o resfriamento de eletrônicos. Contudo, há uma alternativa que envolve a classe dos líquidos perfluorinados que são excelentes dielétricos e têm propriedades da transferência de calor superiores às dos gases.

Considere o resfriamento do chip com microcanais do Problema 8.109, mas agora usando um líquido perfluorinado com as seguintes propriedades: = 1050 J/(kg · K), k = 0,065 W/(m · K), μ = 0,0012 N · s/m² e Pr = 15.

(a) Para dimensões dos canais de H = 200 μm, W = 50 μm e S = 20 μm, uma condutividade térmica do chip de = 140 W/(m · K) e largura do chip de L = 10 mm, uma temperatura na base do canal (x = 0) de = 350 K, uma temperatura na entrada do canal de = 290 K, e uma vazão mássica de por canal, determine a temperatura de saída do líquido dielétrico e a dissipação de potência no chip.

(b) Considere as condições anteriores, mas com o ar com uma vazão de sendo usado como refrigerante. Usando propriedades do ar iguais a = 1007 J/(kg · K), k = 0,0263 W/(m · K) e , determine a temperatura de saída do ar e a dissipação de potência no chip.

Passo 1

Antes de começar o exercício, é interessante dar uma olhada no Problema 8.109 e analisar a geometria do problema, porque a análise aqui será basicamente a mesma. Então vamos lá!

Teremos as laterais dos microcanais agindo como se fossem aletas. Vamos calcular o passo S dos canais através da equação fornecida no enunciado, onde teremos:

Com isso, o espaçamento entre os canais será:

Agora, como vamos tratar as laterais dos microcanais como aletas, temos que a resistência térmica da célula pode ser encontrada através da equação 3.108, dada para um conjunto de aletas, onde temos:

Onde nós temos que:

Substituindo os valores conhecidos, chegamos em:

Passo 2

Agora vamos calcular o diâmetro hidráulico para o nosso sistema, que será dado por:

Então, com isso, podemos encontrar o número de Reynolds, que será dado por:

Sabemos que a vazão mássica pode ser escrita como:

Substituindo essa expressão na equação para Reynolds e substituindo os valores conhecidos, temos:

Dessa forma, sabemos que o escoamento será laminar.

Passo 3

Com o número de Reynolds encontrado no passo 2, temos que o escoamento é laminar. Com isso, vamos consultar a tabela 8.1 vista nessa seção e apresentada a seguir para obter no número de Nusselt para o escoamento:

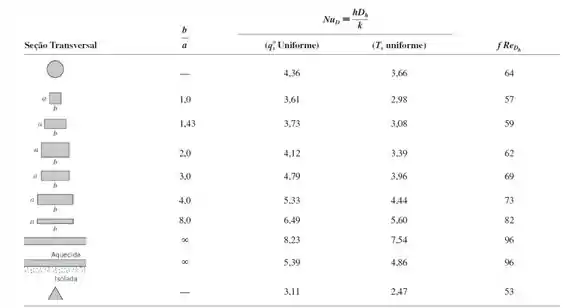
Então, precisamos calcular a razão b/a, onde teremos:

E, como temos uniforme, então no nosso caso teremos:

Com isso, sabendo que o número de Nusselt se relaciona com o coeficiente convectivo através da seguinte relação:

Substituindo os valores conhecidos, temos:

Agora, com isso podemos calcular a eficiência de uma aleta, dada por:

Onde temos:

Substituindo os valores conhecidos, temos:

Então, a eficiência para uma aleta será:

Passo 4

Agora, com a eficiência da aleta, podemos calcular a eficiência geral de superfície, dada por:

Com esse valor, podemos calcular a resistência térmica descrita lá no passo 1, onde teremos:

E, agora, podemos utilizar a equação 8.45b vista nesse capítulo para encontrar a temperatura média de saída. Dessa forma, teremos:

Como no nosso caso, conhecemos a temperatura da superfície externa e ela é constante, a equação se torna:

Substituindo os valores conhecidos, chegamos em:

Agora, com a temperatura de saída, conseguimos encontrar a potência dissipada pelo chip, através do calor trocado com a água, dada por:

Substituindo os valores conhecidos, temos:

Passo 5

Agora, para a letra (b), com o ar com uma vazão de sendo usado como refrigerante. Usando propriedades do ar iguais a = 1007 J/(kg · K), k = 0,0263 W/(m · K) e . Agora devemos repetir os cálculos feitos para a letra (a), então, vamos lá, começando pela área total, como não houve alteração em H e W, a área será a mesma, ou seja:

O diâmetro hidráulico também será o mesmo, mas o número de Reynolds mudará, já que alteramos o fluido, e teremos agora:

O escoamento continua sendo laminar. Teremos também o mesmo valor de Nusselt, já que a temperatura continua constante na superfície e a geometria dos microcanais não mudaram, então teremos: