O diagrama de Moody dá o fator de atrito de Darcy, , em termos do número de Reynolds e da rugosidade relativa. O fator de atrito de Fanning para escoamento em tubo é definido como:
em que é a tensão de cisalhamento na parede do tubo. Mostre que a relação entre os fatores de atrito de Darcy e de Fanning, para escoamento completamente desenvolvido, é dada por .
Passo 1
Neste problema devem ser avaliados os fatores de atrito de Darcy e de Fanning para um escoamento completamente desenvolvido.
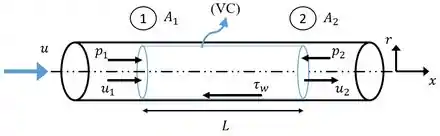
O fator de atrito de Darcy é obtido a partir da Eq. 8.34, a qual retrata a perda de carga ao longo de um escoamento completamente desenvolvido como sendo:
Como hipótese para a resolução do problema são definidas:
- regime permanente ();
- escoamento completamente desenvolvido (
- escoamento horizontal ( e força de campo nula - );
- escoamento incompressível ();
- ;
- seção transversal constante (;
- queda de pressão ;
- tubo de comprimento .
Passo 2
Usando a Equação de Energia, em J/kg, entre as seções 1 e 2:
Então:
Sabendo que , e , a perda de carga é escrita como:
Assim, para escoamento completamente desenvolvimento ao longo de tubulação horizontal a perda de carga é igual a queda de pressão.
Passo 3
Igualando a perda de carga definida no Passo 1 e aquela calculada a partir da Equação da Energia:
Então a queda de pressão é definida como:
Passo 4
O fator de atrito de Fanning foi apresentado em termos da tensão de cisalhamento na parede do tubo, então é necessário aplicar um Balanço de Quantidade de Movimento (relação integral) entre as seções 1 e 2:
Em função das hipóteses do problema, pode-se afirma que o fluxo de quantidade de movimento nas superfícies e são iguais:
Logo:
Passo 5
Sabendo que a equação de Balanço de Quantidade de Movimento se reduziu a:
E que representam as forças de superfície (força devido à pressão e à tensão de cisalhamento), então ela pode ser escrita como:
Nota: sinal positivo no sentido do eixo x.
Então, isolando o termo :
Logo:
Rearranjando o termo de diferença de pressão para escrever o termo queda de pressão (), a tensão de cisalhamento na parede é dada por:
Passo 6
Escrevendo como função de :
Passo 7
Reescrendo a equação de queda de pressão (Passo 3) considerando a expressão de como função de (Passo 6):
Então, o termo pode ser escrito como:
Passo 8
Utilizando a expressão do fato de atrito de Fanning:
E sabendo que:
O parâmetro poderá ser reescrito como:
Então tem-se que:
Ou ainda pode-se afirmar que o fator de atrito de Darcy é dado por: