Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 29
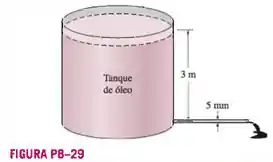
Óleo com densidade de e viscosidade cinemática de é descarregado por um tubo horizontal com de diâmetro e de comprimento de um tanque de armazenamento que está aberto para a atmosfera. A altura do nível do líquido acima do centro do tubo é de . Desprezando as perdas menores, determine a vazão do óleo através do tubo.
Passo 1
O primeiro passo para calcular a vazão volumétrica de óleo através do tubo é calcular o número de Reynolds do escoamento. Se o escoamento for laminar, usaremos uma fórmula para , se ele for turbulento, usaremos outra. A equação do número de Reynolds segue abaixo.
onde é a densidade do fluido (que vale ), é a viscosidade do fluido, (que vale ou ) é o diâmetro do tubo e é a velocidade média do escoamento.
A viscosidade do óleo pode ser calculada a partir da viscosidade cinemática do óleo (que vale ).
Mas como podemos calcular se não sabemos se o perfil de velocidade é turbulento ou laminar? Isso será respondido no próximo passo.
Passo 2
Neste momento nós não precisamos saber o regime de escoamento através do tubo (laminar ou turbulento). Nós podemos calcular supondo inicialmente que o regime é laminar, porque o diâmetro do tubo é muito pequeno (o que resulta em menores e escoamento laminar) e depois calcular o com essa . Se for maior que , o escoamento é turbulento. Se for menor que , é laminar. A fórmula de para um escoamento laminar segue abaixo (equação 8-26 do livro).
onde é o comprimento do tubo (que vale ) e é a perda de pressão através do tubo.
Para calcular a perda de pressão do tubo , precisamos saber qual é a pressão manométrica na entrada do tubo e a pressão manométrica na saída do tubo .
Descobriremos e no próximo passo.
Passo 3
A pressão na entrada pode ser calculada a partir da equação de pressão estática, porque a pressão nesse ponto é causada pela coluna de óleo (de altura ) sobre ele. Logo:
Como o óleo está sendo descarregado para a atmosfera, podemos considerar que a sua pressão é igual a pressão atmosférica. Isso quer dizer que a pressão manométrica val zero.
Substituindo os dados na fórmula de , achamos o valor dessa velocidade.
Substituindo na equação de , achamos:
Como esse é menor que , o escoamento é laminar. Ou seja, podemos usar a laminar que calculamos para calcular .
Passo 4
Podemos calcular através de , multiplicando pela área da seção transversal do tubo ( vale , porque o tubo é circular).