Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 8
Para a distribuição de velocidades do Problema , calcule a circulação sobre a curva fechada retangular definida por , , e . Interprete seu resultado, especialmente diante do potencial de velocidades.
Passo 1
E aí, tudo bem? Bora matar essa questão rapidinho!
Temos a equação do escoamento, vamos montar um esqueminha!
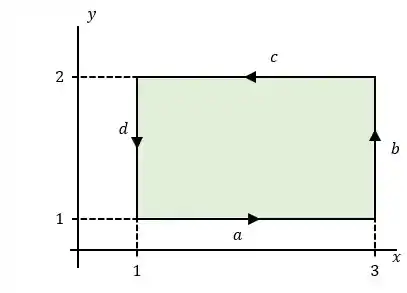
Agora só fazer a integral de linha pro nosso sistema!
Passo 2
Montando os termos temos:
Como:
Como a circulação é igual a zero, podemos afirmar que o escoamento é irrotacional!
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Como a circulação é igual a zero, podemos afirmar que o escoamento é irrotacional!
Exercícios de Livros Relacionados
A componente de velocidade u de um campo de escoamento permanente, bidimensional, incompressível é u =a x+b y , onde a e b são constantes. A componente de velocidade v édesconhecida. Encontre uma expr
Considere o escoamento permanente de água através de um bocal axissimétrico de mangueira de jardim (Figura P9-33).A componente axial da velocidade aumenta linearmente de u e n t r a d a a u s a í d a
São conhecidas duas componentes da velocidade de um campo de escoamento em regime permanente, incompressível: u =a x +b x y + c y 2 e v = a x z - b y z 2 onde a ,b ,ec são constantes. Está faltando a
A componente de velocidade u de um campo de escoamento permanente, bidimensional, incompressível é u =a x 2 -b x y , onde a e b são constantes. A componente de velocidade v é desconhecida. Encontre um
Um bloco desliza para baixo em uma parede longa, reta, inclinada, com a velocidade V , sobre um filme fino de óleo de espessura h (Figura P9-113).O peso do bloco é W ,e sua área de contato com a filme