Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 110

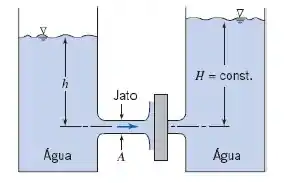
Dois grandes tanques contendo água têm pequenos orifícios de contornos lisos e arredondados e de áreas iguais. Um jato de líquido sai do tanque da esquerda. Considere que o fluxo seja uniforme e não afetado por atrito. O jato atinge uma placa plana cobrindo a abertura do tanque da direita. Determine o mínimo valor da altura, h , requerida para manter a placa no lugar sobre a abertura do tanque da direita.

Passo 1

Tá legal! Vamos começar o exercício aplicando Bernoulli entre a superfície h e a saída do jato, dessa forma, temos:

p s ρ + v s 2 2 + g h = p j ρ + v 2 2 + g ( 0 )

Então como estamos considerando os tanques como sendo de grandes dimensões, temos v s = 0 , e como a superfície e o jato estão expostos ao ambiente, então p s = p j = 0 , substituindo os valores conhecidos, temos:

0 ρ + 0 2 2 + g h = 0 ρ + v 2 2 → v = 2 g h

Agora vamos calcular a pressão exercida pela coluna d’água do tanque da direita na altura do jato, sabemos que ela é dada pelo seu peso multiplicado pela altura da coluna, que nesse caso é a altura H , então:

p = ρ g H

Passo 2

Agora podemos aplicar a equação da quantidade de movimento 4.18a apresentada nessa seção para o volume de controle destacado a seguir:

F x = F S x + F B x = ∂ ∂ t ∫ V C   u ρ d V + ∫ S C   u ρ V → . d A →

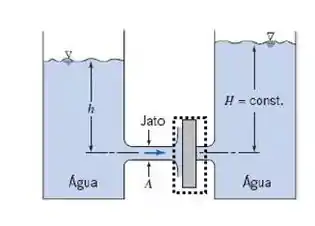
Então, como não temos forças de campo F B x = 0 e também já que o escoamento se dá em regime permanente, a primeira integral com derivada no tempo também é zero, dessa forma, substituindo os valores conhecidos, temos:

- p A = u 1 - ρ v A + u 2 ρ v A

Já encontramos o valor da pressão p exercida pelo tanque da direita, e sabemos que u 1 = v e u 2 = 0 , então, substituindo os valores conhecidos:

- ρ g H A = v - ρ v A + 0 ρ v A → - ρ g H A = - v 2 ρ A

H = v 2 g

Passo 3

Agora vamos substituir o valor de v encontrado através de Bernoulli no passo 1, então:

H = 2 g h 2 g → H = 2 g h g → h = H 2

Resposta

h = H 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deseja-se uma bomba que, acoplada a um motor de 3450 rpm, produza uma altura manométrica teórica de 80 m. O ângulo de entrada das pás deve ser de 15º e o de saída, de 30º. Sendo d 1 = 10c m , quanto d
Uma bomba centrífuga tem pás com ângulo de entrada 15º e de saída de 25º. A rotação é 1720 rpm e os diâmetros de entrada e saída são, respectivamente, de 10cm e 25cm. Sendo v u 1 = 0 e v r 1 = v r 2 ,
No dispositivo da figura, o pistão de peso G = 29,4k N desce muito lentamente dentro do cilindro de área 2m 2 , empurrando a água ( γ = 10 4N / m 3 ) pelos dois cotovelos instalados simetricamente. A
O tampão de base circular da figura está colocado concentricamente na tubulação horizontal de seção circular para controlar a vazão de água. Sendo ρ = 1000k g / m 3 e desprezando a perda de carga, det
Duas bombas recalcam água ( γ = 10 4 N / m 3 ) para o sistema da figura, no qual é lançada na vertical para a atmosfera, na seção 4 . O tubo de saída é isolado do resto da instalação por uma luva elás