Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 111
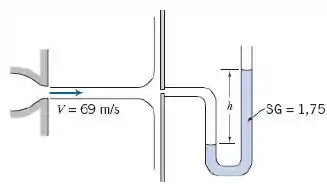
Um jato de ar horizontal com 13 mm de diâmetro, e axialmente simétrico, atinge um disco estacionário vertical com 203 mm de diâmetro. A velocidade do jato é de 69 m/s na saída do bocal. Um manômetro está conectado ao centro do disco. Calcule (a) a deflexão, , se o líquido do manômetro tem densidade relativa SG = 1,75 e (b) a força exercida pelo jato sobre o disco.
Passo 1
Tá legal! Vamos começar o exercício aplicando Bernoulli entre a a saída do bocal e o ponto de estagnação no disco:
Sabemos que o ponto de estagnação é definido por ter , então, substituindo esse valor na equação anterior, temos:
Passo 2
No entanto, agora podemos aplicar a equação de equilíbrio manométrica para o manômetro do problema, de modo que:
Então, substituindo esse valor na última equação do passo 1, temos:
Substituindo os valores conhecidos, temos a deflexão pedida na letra a):
Passo 3
Para resolver a letra b) vamos aplicar a equação 4.18a apresentada nessa seção do equilíbrio de momento para o volume de controle ilustrado a seguir:
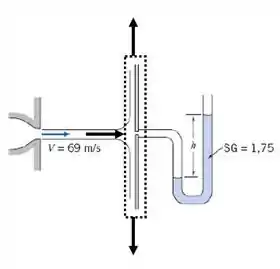
Como não temos força de campo na direção então e como o escoamento se dá em regime permanente, então a derivada no tempo também será zero, dessa forma, substituindo os valores conhecidos, temos:
No entanto, a velocidade de aproximação , então, substituindo esse valor na equação anterior:
A área é a área do jato, que é circular, então:
Substituindo os valores conhecidos:
Então, a força de reação na placa possuirá a mesma intensidade, só que sentido oposto, então: