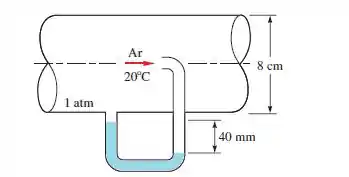
Para a combinação de tubo de Pitot e tomada de pressão estática (tubo de Pitot estático) na figura abaixo, o líquido manométrico é água (colorida) a 20°C. Calcule (a) a velocidade na linha de centro, (b) a vazão volumétrica e (c) a tensão de cisalhamento na parede (lisa).

1. Bem vamos aqui usar a nossa vela e boa hidrostática para podermos calcular qual deve ser a queda de pressão para depois usarmos a equação que relaciona a velocidade no centro com a queda de pressão:

Percebe que precisamos da diferença de pressão nos pontos né?

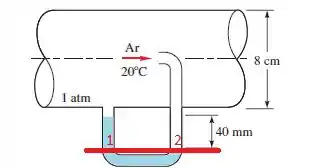
Agora vamos substituir essa diferença de pressão na nossa equação de

(b) Podemos também estimar o fator de atrito e depois computar a velocidade média, se liga como!

Vamos chutar que a nossa velocidade média seja em torno de 85% da velocidade no centro, então:

Aí o que a gente faz? Calcula o número de Reynold para esse escoamento:

Vamos estimar também um valor de f = 0,0175 e aí no livro tem uma equação que expressão a relação de velocidade média com a velocidade máxima, que é:

Ou seja, você perceber bem essa velocidade obtida pela equação acima convergiu com aquela que chutamos inicialmente. Note que o nosso raciocínio aqui foi: chutar um valor de velocidade média, calcular Reynold, obter mais ou menos um valor de f em uma das curvas do diagrama de Moody e com isso descobrir a nova velocidade média pela equação acima.

Portanto, como temos a velocidade convergida, conseguimos calcular nossa vazão volumétrica, pois:

(c) Finalmente, a tensão de cisalhamento na parede pode ser dada por: