Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 61

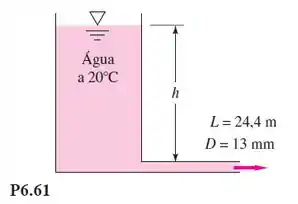
Qual nível h deve ser mantido na Figura P6.61 para fornecer uma vazão de 0,425 L/s pelo tubo de aço comercial de 13 mm de diâmetro?

Passo 1

Eeeeeee vamo nessa!

Bora lá, tamo careca de saber que para a água ρ = 998   k g / m 3 e μ = 0,001   k g / ( m ⋅ s ) , e, transformando a vazão, teremos Q = 0,000425   m 3 / s . Assim, comecemos encontrando a velocidade:

V = Q A = 0,000425 m 3 s π 4   0,013   m 2 = 3,20   m / s

Belê, partindo agora para Reynolds, teremos:

R e = ρ V D μ = 998 k g m 3 3,20 m s 0,013   m 0,001   k g / ( m ⋅ s ) ≈ 41500

Tendo a nossa rugosidade relativa de um tubo comercial sendo:

ϵ D = 0,046   m m 13   m m = 0,00354

Daí, pelo Diagrama de Moody, encontraremos nosso fator de atrito sendo:

f = 0,030

Passo 2

Agora, faremos nossa equação de energia, temos:

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 2 g + z 2 + h f

Temos que ambos os lados estão abertos para a atmosfera, assim, as pressões irão se anular! Considerando V 1 = 0 , pois D 1 ≫ D 2 , teremos:

h = h f + V 2 2 2 g

Sendo,

h f = f L D V 2 2 2 g

Teremos:

h = V 2 2 g 1 + f L D

Substituindo,

h = 3,20 m s 2 2 9,81 m s 2   1 + 0,030   24,4   m 0,013   m = 29,9   m

Resposta

29,9   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é o diâmetro hidráulico? Como é determinado? A que ele é igual para ura tubo circular de diâmetro D?
Considere uma pessoa caminhando primeiro no ar e depois na água à mesma velocidade. Para qual movimento o número de Reynolds será mais alto?
Mostre que o número de Reynolds para o escoamento em um tubo circular de diâmetro D pode ser expresso como: R e = 4 m ˙ π D μ
Sabe-se que estão presentes condições plenamente desenvolvidas no escoamento de água, com vazão de 0,02k g / s e a 27 ° C , em um tubo com 5 0m m de diâmetro. Qual é a velocidade máxima da água no tub
Quando a água a 20°C está em escoamento turbulento permanente por um tubo de 8 cm de diâmetro, a tensão de cisalhamento na parede é 72 Pa. Qual é o gradiente de pressão axial (dp/dx), se o tubo estive