Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 145
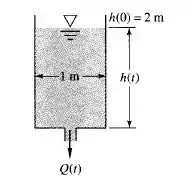
O reservatório de 1 m de diâmetro na figura abaixo está inicialmente cheio de gasolina a 20°C. Existe um orifício de 2 cm de diâmetro no fundo. Se o orifício é aberto repentinamente, calcule o tempo para o nível de fluido h(t) baixar de 2,0 para 1,6 m.
Passo 1
E ai, galera! Tranquilidade? Bora que bora encarar mais um desafio?
Primeiro vamos pegar as propriedades da gasolina a 20°C!!!
Agora bora lá, a gente sabe que esse trem aí tá parecendo que vamos precisar usar aquela equação para orifícios, então um parâmetro muito importante é o que é a razão entre o diâmetro do orifício e o diâmetro do tubo ou tanque, ou seja lá por onde o fluido esteja escoando. Note que aqui , pois o diâmetro do tanque é muitooo maior que o diâmetro do orifício.
Passo 2
Precisamos encontrar quem é nosso valor de !!! Bem, esse cara a gente pode tomar a partir da equação 6.112 do livro que é:
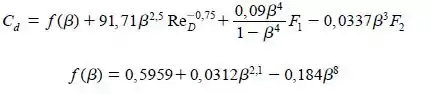
Podemos considerar que , pois estamos tomando tomadas em cantos. Mas note que eu precisaria de Reynold né? Então o que a gente faz? Chutamos um valor de que é um valor típico para orifícios.
Substituindo então na nossa equação do passo 1 e lembrando que , temos:
Passo 3
Pelo balanço de massa temos ainda que:
Onde que encontramos no passo anterior, então, vamos seguir!!
Vamos precisar integrar na altura e no tempo! Beleza, o tempo é só integrar de 0 até um tf. Mas e a altura? Bem, ela precisará ser integrada de 2 até 1,6m, pois queremos saber o tempo que demorará para fazer essa diminuição de altura!!!