Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 69

Duas bolas de beisebol do Problema 7.68 são conectadas a uma barra de 7 mm de diâmetro e 56 cm de comprimento, como na figura abaixo. Qual a potência, em W, necessária para manter o sistema girando a 400 rpm? Inclua o arrasto da barra e admita ar padrão ao nível do mar.

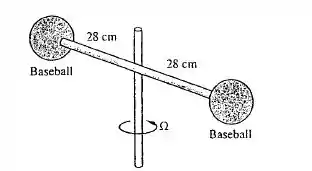
Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

(a) Vamos lá, essa questão é mais trabalhosa do que difícil!!!! Então bora que bora!!

Primeira coisa que vou fazer é pedir pra você pegar as propriedades do ar no nível do mar, show?

ρ = 1,225   k g / m ³

μ = 1,78   x   10 - 5   k g / ( m . s )

E da tabela 7.3 para essa situação de uma bola de beisebol a gente vai obter que C D ≈ 0,47 . Convertendo também nossa velocidade angular Ω = 400   r p m   x 2 π 60 = 41,9   r a d / s .

Cada bola vai girar numa velocidade na linha de centro com:

V b = Ω r b = 41,9   0,28 + 0,0735 2 = 13,3   m / s

Checando o valor de Reynold vamos obter que:

R e = ρ V b D / μ = 1,225 13,3 0,0735 1,78   x   10 - 5 = 67000

Ou seja, pela tabela 7.3 temos que C D = 0,47

Passo 2

A força de arrasto em cada bola de baseball é aproximadamente em torno de:

F D = C D ρ 2   V b 2 π 4 D 2 = 0,47   1,225 2 13,3 2 π 4   0,0735 2 = 0,215   N

Passo 3

Similarmente para a barra, temos que calcular sua velocidade e estimar um coeficiente de arrasto para depois ver qual é a força de arrasto!!!

V r = Ω r m é d i o = 41,9 0,14 = 5,86   m / s

R e = ρ V r d μ = 1,225 5,86 0,007 1,78   x   10 - 5 = 2800 → C D = 1,2   t a b e l a   7.3

F b a r r a = C D   ρ 2 V r 2 D L = 1,2 1,225 2 5,86 2 0,007 0,28 = 0,0495   N

Passo 4

Então a potência total deve ser dada por:

P o t = 2 F b V b + 2 F r V r

P o t = 2 0,215 13,3 + 2 0,0495 5,86 = 5,71 + 0,58 = 6,3   W

Note que o fator “2” que aparece é porque temos duas bolas de baseball e duas barras de 28 cm!!

Resposta

P o t = 6,3   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando imersa em um escoamento uniforme V, uma barra pesada articulada em A se deslocará ao ângulo de Pode, u, de acordo com a análise de L. Pode em 1951 (Figura P7.103). Suponha que o cilindro tenha
Partículas de areia (d = 2,7) aproximadamente esféricas, com diâmetros entre 100 mm e 250 mm, são introduzidas em uma corrente ascendente de água a 20°C. Qual é a velocidade mínima da água que levará
Um ciclista de nível internacional pode gerar 0,5 hp por longos períodos. Para uma prova ao nível do mar, calcule a velocidade que esse ciclista pode manter. Despreze o atrito de rolagem.
À medida que os soldados vão ficando maiores e as mochilas mais pesadas, um paraquedista e sua carga podem chegar a pesar até 1780 N. O paraquedas padrão de 8,5 m pode descer rápido demais para a segu