Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 102

Partículas de areia (d = 2,7) aproximadamente esféricas, com diâmetros entre 100 mm e 250 mm, são introduzidas em uma corrente ascendente de água a 20°C. Qual é a velocidade mínima da água que levará todas as partículas de areia para cima?

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos partículas de areia de massa específica 2700   k g / m ³ com diâmetros variando de 100   μ m a 250   μ m que são introduzidas em uma corrente de água de massa específica ρ = 998   k g / m ³ e viscosidade μ = 1 × 10 - 3 P a ∙ s .

O enunciado nos pede pra calcular a velocidade mínima pra levar todas as partículas pra cia, ou seja, é necessário uma força suficiente pra levar as partículas maiores de diâetro D = 2 , 5 × 10 - 4   m , e as menores seguirão junto.

Pra resolver a questão, vamos lembrar que para um sistema em equilíbrio, o peso W das partículas será igual a sua força de arrasto F A .

W = F A → C A ρ V 2 2 π 4 D 2 = W  

Dessa relação, podemos tirar a o valor de C A V ² :

C A V 2 = W ρ π 4 D 2 = 2 2700 k g m 3 - 998 k g m ³ π 6 2 , 5 × 10 - 4   m ³ 9,81   m / s ² 998   k g / m ³ π 4 2,5 × 10 - 4   m ² = 0,0055   m 2 / s ²

Passo 2

Pra calcular o valor da velocidade, devemos ir na Figura 7.16(b) na página 492.

Pra isso, vamos usar um método iterativo utilizando a relação C A V 2 = 0,0055   m 2 / s ² deduzida na página anterior. Vou te mostrar um fluxograma detalhado de como fazer isso:

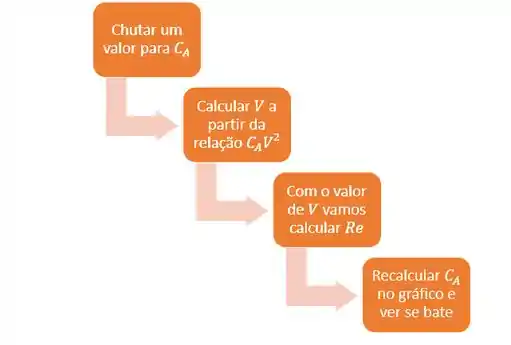
Pra essa resolução não se estender demais, a gente vai mostrar o resultado direto pra você:

R e = 10

C A ≈ 4,0

V ≈ 0,04   m / s

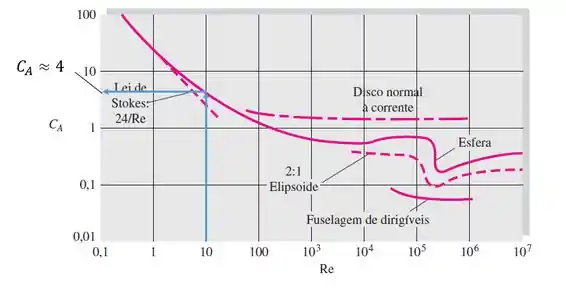
Pronto, matamos o problema juntos!

Resposta

A velocidade necessária do jato é V = 0,04   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um paraquedas típico do Exército norte-americano tem um diâmetro projetado de 8,5 m. Para uma carga total com massa de 80 kg, (a) qual é a velocidade terminal resultante na altitude padrão de 1.000 m?
Considere os paraquedistas acrobatas, voando acima do nível do mar. Em geral, eles saltam a cerca de 2.400 m de altitude e realizam queda livre de peito, com braços e pernas abertos, até abrirem seus
Um carro em alta velocidade tem um coeficiente de arrasto de 0,3 e área frontal de 1 m2. Um paraquedas é usado para reduzir a velocidade desse carro de 80 m/s para 40 m/s em 8 s. Qual seria o diâmetro
Um caminhão com cavalo mecânico e baú tem uma área de arrasto própria CAA = 8 m2 e 6,7 m2 com um defletor aerodinâmico (Figura 7.18b). Sua resistência de rolagem é de 50 N para cada quilômetro/hora de
Uma bola de tênis de mesa pesa 2,6 g e tem um diâmetro de 3,8 cm. Essa bola pode ser sustentada por um jato de ar na saída de um aspirador de pó, como na Figura 7.84. Para ar padrão ao nível do mar, q