Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 103

Quando imersa em um escoamento uniforme V, uma barra pesada articulada em A se deslocará ao ângulo de Pode, u, de acordo com a análise de L. Pode em 1951 (Figura P7.103). Suponha que o cilindro tenha coeficiente de arrasto normal CAN e coeficiente tangencial CAT que relacionam as forças de arrasto a VN e VT, respectivamente. Deduza uma expressão para o ângulo de Pode em função dos parâmetros do escoamento e da barra. Determine u para uma barra de aço com L = 40 cm e D = 1 cm, inclinando-se no ar ao nível do mar com V = 35 m/s.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Vamos deduzir uma expressão para o ângulo θ

Primeiro, começamos olhando o esquema abaixo pra ver as forças agindo na barra:

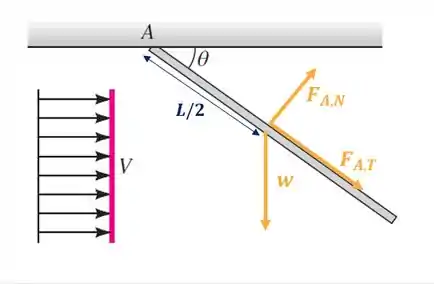
Podeos fazer um balanço de momento da componente normal da força de arrasto F A , N   e do peso W com relação ao ponto A, que deve ser igual ao zero para o sistema estar em equilíbrio:

∑ M A = 0 = F A , N   L 2 - W L 2 cos ⁡ θ

C A , N   ρ 2 V sin ⁡ θ 2 D L L 2 - ρ s - ρ g π 4 D ² L L 2 cos ⁡ θ = 0

Reorganizando a equação, podemos encontrar a expressão para θ :

sin 2 ⁡ θ cos ⁡ θ = ρ s - ρ g π D 2 ρ C A , N V ²

Passo 2

Agora, vamos exemplificar a resolução da equação deduzida com valores numéricos.

Primeiro, devemos considerar as propriedades do ar como ρ = 1,2   k g / m ³ e μ = 1,8 × 10 - 5 P a ∙ s .

Vamos calcular o Número de Reynolds:

R e = ρ V D μ = 1,2 k g m 3 35 m s 0,01   m 1,8 × 10 - 5 P a ∙ s = 2,92 × 10 4

Como escoamento é laminar de L D = 40 , indo na Tabela 7.3, teremos C A , N ≈ 1,2 .

Como a barra é de aço, ρ s = 7860   k g / m ³ .

Substituindo o valor numérico:

sin 2 ⁡ θ cos ⁡ θ = ρ s - ρ g π D 2 ρ C A , N V ² = 7860 k g m 3 - 1,2 k g m 3 9,81 m s 2 π 0,01   m 2 1,2 k g m 3 1,2 35   m / s 2

θ ≈ 44 °

Pronto, matamos a questão juntos!

Resposta

O ângulo formado pela barra é θ ≈ 44 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É difícil definir a “área frontal” de uma motocicleta devido ao seu formato complexo. Mede-se então a área de arrasto (ou seja, CAA), em unidades de área. Hoerner [12] relata que a área de arrasto de
Para medir o arrasto de uma pessoa em posição ereta, sem violar protocolos de segurança, um manequim do tamanho da pessoa é fixado à extremidade de uma barra de 6 m e posto para girar a Ω = 80 rpm, co
Aplique o Problema 7.61 a um filtro que consiste em um pacote de 250 fibras por centímetro quadrado, cada qual com 300 μm de diâmetro, no plano da Figura P7.61. Para o ar a 20oC e 1 atm escoando a 1,5
Suponha que uma partícula de poeira radioativa se assemelhe a uma esfera de massa específica 2.400 kg/m3. Quanto tempo, em dias, levará tal partícula para descer de uma altitude de 12 km até o nível d
Uma esfera pesada fixada em uma corda se deslocaria um ângulo θ quando imersa em uma corrente de velocidade U, como na Figura P7.80. Deduza uma expressão para u em função das propriedades da esfera e