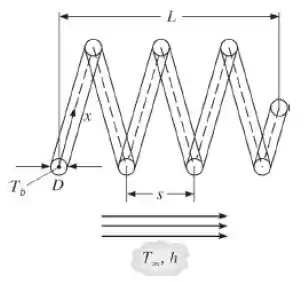
Durante os estágios iniciais do crescimento do nanotubo do Problema 3.109, uma pequena perturbação na gota do catalisador líquido pode causar um deslocamento fazendo com que ela fique suspensa na extremidade do nanofio fora da posição central. A deposição não uniforme resultante do sólido na interface sólido-líquido pode ser manipulada para gerar formas específicas como uma nanomola, que é caracterizada por um raio da mola, r, um passo da mola, s, um comprimento total, L t (comprimento ao longo da mola), e um comprimento entre as extremidades, L, como mostrado no esboço. Seja uma nanomola de carbeto de silício de diâmetro D = 15n m ,r = 30n m , s = 25n meL t = 425n m . A partir de experimentos, sabe-se que o passo médio da mola S - varia com a temperatura média T - de acordo com a relação d S - d T - = 0,1 n m K . Usando esta informação, um estudante sugere que um nanoatuador pode ser construído conectando-se uma extremidade da nanomola a um pequeno aquecedor e elevando-se a temperatura dessa extremidade acima do seu valor inicial. Calcule a distância de atuação (alcance), ΔL, para condições nas quais h×10 6 W m 2 K ,T ∞= T i= 25 ° C , com uma temperatura na base de T b = 50 ° C . Se a temperatura na base puder ser controlada na faixa de 1°C, calcule a precisão na qual a distância de atuação poderá ser controlada. Sugestão: Suponha que o raio da mola não mude quando ela é aquecida. O comprimento total da mola pode ser aproximado pela fórmula, L = s 2 π . L c r 2 + s 2 π 2

Enunciado

Esta parece ser cabulosa galeraa, mas a gente vai tirar de letra, ein !!

Nós queremos a precisão na qual a distância de atuação poderá ser controlada, se a temperatura na base puder ser controlada na faixa de 1°C:

A temperatura inicial nós já temos, então só precisamos de .

Para calcular esta variação do comprimento nós vamos começar calculando o comprimento quando então , quando nós substituímos na equação dada:

Sabendo que:

Agora é só substituir:

Mas não achamos o que queríamos, certo?

Já sabemos que o passo médio da mola varia linearmente com a temperatura média, então:

Agora nós precisamos achar o excesso de temperatura médio:

Lembrando que:

Então:

Aplicando o intervalo:

Vamos começar calculando nossos dados:

E sabendo que:

Mas não temos k, certo? Usando a tabela A.1 o valor obtido para 300 K que se aproxima da nossa temperatura média:

Calculando:

Agora é só achar

Substituindo em

Agora é só colocar na fórmula de :

Bom galerinha, já temos o novo valor de s, então agora é só calcular o novo comprimento:

No Passo 1 nós vimos que:

Substituindo:

Ufaaaa !! Terminamos mais umaa !!

Estão felizes que eu sei