Sem dúvida, você usou a fórmula do ressalto horizontal para resolver o Problema , o que é razoável, já que a declividade é muito pequena. No entanto, Chow destaca que os ressaltos hidráulicos são mais altos sobre canais em declive, devido ao “peso do fluido no ressalto”. Faça um esquema de um volume de controle de um ressalto hidráulico em declive para mostrar por que isso acontece. O diagrama do ressalto em declive dado na Figura do texto de Chow pode ser aproximado pelo seguinte ajuste de curvas:
em que é a faixa de declividade dos canais para os quais há dados disponíveis. Use essa correlação para modificar a sua solução do Problema . Se houver tempo suficiente, faça um gráfico de em função do para vários .
Passo 1
E aí, tudo bem? Bora matar essa questão!
Antes de tudo vamos fazer o esqueminha que a questão nos pede!
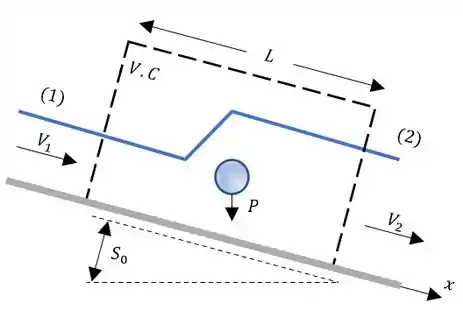
Agora vamos fazer o somatório de forças para nosso sistema!
Mas temos que lembrar que:
Passo 2
Agora a gente vai suar um pouco a camisa pra organizar essas equações, mas não desista! Bora!
Substituindo temos:
Vale lembrar:
Assim:
Lembrando que:
Substituindo mais uma vez!
Agora vamos começar a organizar!
Nesse ponto eu tô nesse estado:

Passo 3
Vamos chamar de , assim:
Vamos multiplicar tudo por
Agora só organizar essa equação:
Onde:
Lembrando que pra ângulos pequenos !
Agora só precisamos entender pra que tanta conta meu pai amado!
A solução da equação nos dá a taxa da altura do ressalto , se , se , a altura do ressalto aumentará de forma grosseira como a formula de Chow nos diz. Então só teremos uma pequena variação se comparado ao que encontramos na questão
Passo 4
Vamos avaliar a mudança do resultado que encontramos:
Passo 5
Agora só precisamos montar um gráfico com os dados que o problema nos dá!

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta
Gráfico vide passo a passo