Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 102

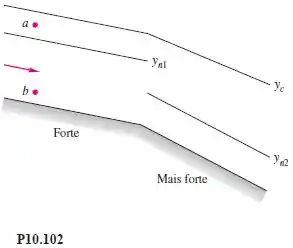
O escoamento em canal largo na Figura muda de uma declividade forte para outra ainda mais forte. Começando nos pontos e , faça um esboço e identifique os perfis de superfície da água esperados para escoamento gradualmente variado.

Passo 1

E aí, tudo bem? Bora matar essa questão!

Essa é bem simples, vamos trabalhar com possibilidades, mas vamos usar a lógica, primeiro vamos avaliar nosso problema!

Para o esquema e :

Da figura nossos escoamentos se classificam respectivamente como e

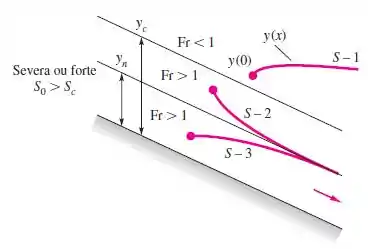
Como o aumento do declive não altera sua classificação tendo em vista a permanência de , já se for alto o suficiente ele ficará acima de logo será , caso contrário continuará sendo agora só desenhar o esquema!

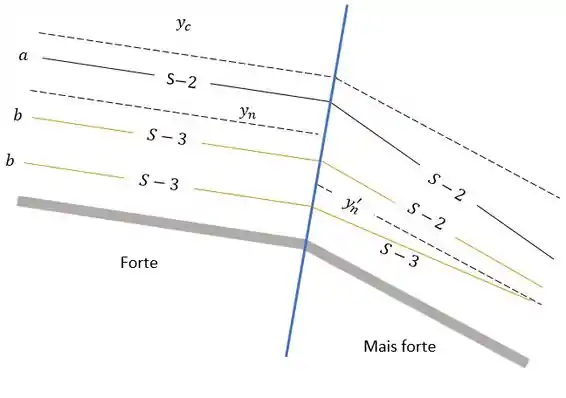
Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

Gráfico e explicação videm passo a passo

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sem dúvida, você usou a fórmula do ressalto horizontal ( 10.43 ) para resolver o Problema P 10.89 , o que é razoável, já que a declividade é muito pequena. No entanto, Chow [ 2 ,p .425 ] destaca que o

A Figura P 10.113 mostra uma contração de seção em um canal, às vezes chamada de calha venturi [ 23 ,p .167 ] porque as medidas de y 1 e y 2 podem ser usadas para medir a vazão. Mostre que, se as perd

Água flui a 1,5m 3 / s ao longo de um canal reto, rebitado, em forma de V de 90 ° (ver Figura 10.41 , θ = 45 ° ). Na seção 1 , a profundidade da água é 1,0m . (a) À medida que caminhamos a jusante, a

A teoria de escoamento gradualmente variado, Equação (10.49), despreza o efeito das variações de largura, db/dx, admitindo que elas são pequenas. Mas elas não são tão pequenas para uma contração curta

Resolva o Problema P10.105 (uma variação horizontal ao longo de uma curva H-3) pelo método aproximado da Equação (10.52), começando em (x, y) = (0, 0,246 m) e usando um incremento de profundidade Dy =