Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 53
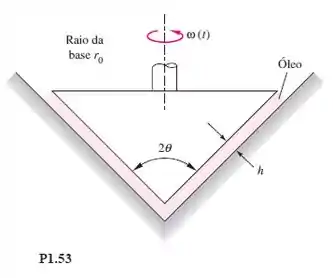
Um cone sólido de ângulo , base e massa específica está girando com velocidade angular em um assento cônico, como mostra a Figura . A folga é preenchida com óleo de viscosidade . Desprezando o arrasto do ar, deduza uma expressão analítica para a velocidade angular do cone se não há torque aplicado.
Passo 1
Vamos lá, podemos montar a formula para o torque diferencial.
Onde:
Assim:
Agora temos que integrar nosso torque, vamos lá!
Passo 2
Agora podemos abordar o torque em função do momento angular, assim temos:
Onde é a massa do cone.
Passo 3
Agora separando as variáveis e após vamos integrar.
Estamos quase lá, não desistam!
Aplicando a exponencial finalmente achamos a função da velocidade!
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Exercícios de Livros Relacionados
Mott [Referência 49, p.38] apresenta um viscosímetro simples de queda de esfera, que podemos analisar mais tarde no Capítulo 7. Uma pequena esfera de diâmetro D e massa específica ρ e cai através de u
A alavanca da Figura A1.9 tem um peso P em uma das extremidades e está presa a um cilindro na outra extremidade. O cilindro tem peso e empuxo desprezíveis e desliza para cima em um filme de óleo pesad
Óleo SAE 10 W a 20 °C escoa ao longo de uma superfície plana, como mostrado na Figura 1.6b. O perfil de velocidade u y é medido, obtendo-se os seguintes resultados:Usando as suas melhores habilidades
Um dispositivo mecânico que usa o cilindro rotativo da Figura A1.6 é o viscosímetro Stormer [29]. Em vez de ser acionado a uma velocidade angular constante Ω , uma corda é enrolada ao redor do eixo e
O viscosímetro de cilindro rotativo na Figura A1.6 provoca cisalhamento no fluido em uma folga pequena Δ r , como mostra a figura. Considerando uma distribuição linear de velocidade nas folgas e medin