Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 98
Um elemento combustível de um reator nuclear é constituído por um bastão cilíndrico maciço de raio e condutividade térmica . O bastão combustível encontra-se em perfeito contato com um material de revestimento que possui um raio externo e uma condutividade térmica . Suponha condições de regime estacionário, nas quais há geração uniforme de calor no interior do combustível a uma taxa volumétrica e a superfície externa do revestimento está exposta a um refrigerante caracterizado por uma temperatura e um coeficiente convectivo h.
(a) Obtenha equações para as distribuições de temperaturas e no combustível e no revestimento, respectivamente. Expresse os seus resultados exclusivamente em termos das variáveis anteriores.
(b) Seja um bastão combustível de óxido de urânio, com e , e um revestimento com e . Se , h = 2000 W/(m2 · K) e = 300 K, qual é a temperatura máxima no elemento combustível?
(c) Calcule e represente graficamente a distribuição de temperaturas, T(r), para valores de h = 2000, 5000 e 10.000 W/(m² · K). Se a operadora desejar manter a temperatura no eixo central do elemento combustível abaixo de 1000 K, ela poderá fazer o controle ajustando o escoamento
do refrigerante e desta forma o valor do h?
Passo 1
Beleza! Antes de começar a letra (a), devemos ilustar o problema com o que foi fornecido no enunciado, então, teremos:
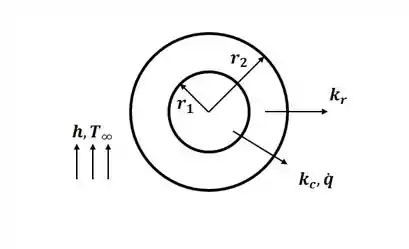
Então, como temos geração no bastão interno e não temos no externo, devemos separar o problema em duas partes. Teremos uma equação para o perfil de temperatura na parte interna e outra na parte externa. Então, na parte com geração, a equação da distribuição de temperatura será:
Essa será nossa equação 1 para o raio interno. Agora, para o raio externo, a equação que descreve o perfil de temperatura será:
Essa será nossa equação 2, que representa o perfil de temperatura entre e . Então agora nós vamos integrar nossa equação 1, obtida anteriormente, fazendo isso, chegamos em:
Integrando essa equação novamente, temos:
Agora, integrando nossa equação 2, temos:
Integrando a expressão novamente, chegamos em:
Passo 2
Agora vamos utilizar as condições de contorno conhecidas para determinar as 4 constantes. Então, temos primeiro que não teremos gradiente de temperatura no centro do bastão interno, então, podemos escrever:
Substituindo esses valores na expressão obtida no passo 1, temos:
Uma outra condição de contorno que temos é que a temperatura na superfície é igual para os dois materiais, então, temos:
Substituindo as expressões em , temos:
Essa será nossa equação número 3. Agora, aplicando um equilíbrio de energia em , notamos que toda a energia por condução do bastão também será a energia por condução na camada externa, então, pela lei de Fourier, podemos escrever:
Substituindo as expressões conhecidas, temos:
Agora, a última condição de contorno é dada por um equilíbrio de energia na superfície externa, onde a transferência de calor por condução será igual à de convecção e podemos escrever:
Substituindo as expressões conhecidas, temos:
Isolando chegamos em:
E, substituindo as expressões conhecidas na equação 3, chegamos numa expressão para :
Então, isolando , temos:
Então, substituindo as expressões para as constantes, chegamos em:
E, para a equação entre e temos:
Passo 3
Agora, para a letra (b), nós vamos substituir os valores conhecidos no perfil de temperatura para o bastão interior em , pois é nessa posição que temos a maior temperatura, então, teremos:
Passo 4
Agora, para a letra (c), vamos pegar os perfis de temperatura obtidos no passo 2 e variar os valores de , fazendo isso, teremos:
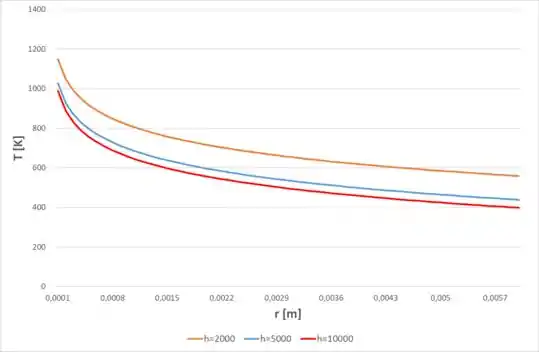
Como podemos observar, o controle no eixo central do combustível não é muito afetado com o incremento de , precisaríamos alterar a condutividade do bastão interno para diminuir essa temperatura.