Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 97
Na figura é mostrada a seção transversal de um elemento combustível cilíndrico longo em um reator nuclear. Geração de energia ocorre uniformemente no bastão combustível de tório, que possui diâmetro D = 25 mm e é envolto por um fino revestimento de alumínio.
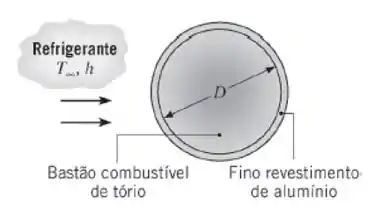
(a) É proposto que, em condições de regime estacionário, o sistema opere com uma taxa de geração de e um sistema de resfriamento caracterizado por e . Essa proposta é satisfatória?
(b) Explore o efeito de variações em e h, representando graficamente distribuições de temperaturas, T(r), para uma faixa de valores dos parâmetros. Sugira um envelope de condições operacionais aceitáveis.
Passo 1
Beleza! A primeira coisa que devemos notar para a letra (a) é que o sistema não irá atender os requisitos quando o um dos elementos entrar em fusão. Então, recorrendo as tabelas do apêndice A do livro, temos que os pontos de fusão do alumínio e do tório são:
Nós sabemos que a temperatura máxima para o tório se dará no centro do cilindro. Então, da equação de distribuição de temperatura (3.58) vista nessa seção para sistemas radiais com geração de calor, temos:
Como nós já vimos, a temperatura máxima ocorre no centro, ou seja, em , então, a equação acima se torna:
Passo 2
Beleza, agora vamos analisar a temperatura para o alumínio, que será a temperatura na superfície, que é dada pela equação 3.60, então, temos:
Substituindo os valores conhecidos, chegamos em:
Agora, substituindo os valores conhecidos na equação para a temperatura máxima do tório encontrada no passo 1, temos:
Então, comparando os valores obtidos com as temperatura de fusão descritas no passo 1, vemos que o tório não irá fundir, no entanto o alumínio vai. Então a proposta não é satisfatória.
Passo 3
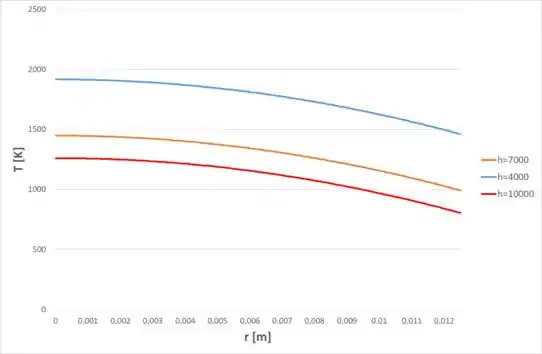
Agora, para a letra (b), vamos primeiro manter constante e variar , então, teremos o seguinte comportamento para o sistema:
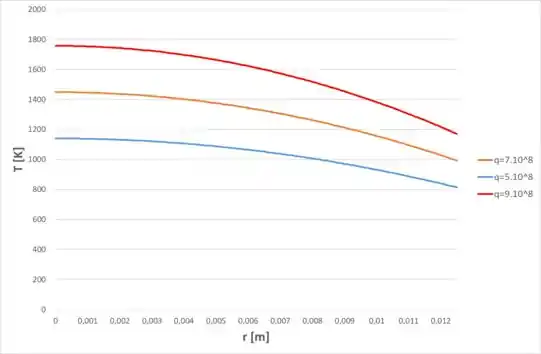
Agora, vamos manter constante e variar o coeficiente de convecção , dessa forma, o comportamento do sistema será:
