Um reator nuclear de alta temperatura com resfriamento a gás é formado por uma parede cilíndrica composta, na qual um elemento combustível de tório (k ≈ 57 W/(m · K)) encontra-se envolto em grafite (k ≈ 3 W/(m · K)) e hélio gasoso escoa através de um canal anular de resfriamento. Considere condições nas quais a temperatura do hélio é de = 600 K e o coeficiente convectivo na superfície externa do grafite é de h = 2000 W/(m² · K).
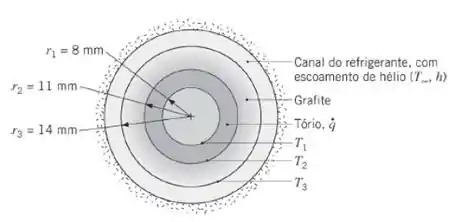
(a) Se energia térmica é gerada uniformemente no elemento combustível a uma taxa , quais são as temperaturas e nas superfícies interna e externa, respectivamente, do elemento combustível?
(b) Calcule e represente a distribuição de temperaturas na parede composta para valores selecionados de . Qual é o valor máximo permissível para ?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado quer que a gente determine as temperaturas e nas superfícies interna e externa, respectivamente, do elemento combustível, e que a gente calcule a distribuição de temperaturas e o valor máximo permissível para .
Pra isso, nós vamos encontrar na superfície externa do combustível (em ) usando as resistências térmicas por unidade de comprimento:
Depois, vamos resolver a equação diferencial no combustível (região ) com geração volumétrica e aplicar as condições de fluxo radial nulo na superfície interna (isolamento):
E a condição de continuidade de temperatura em :
Vamos lá!
Passo 2
Beleza! Para encontrar a temperatura nas superfícies e , nós vamos utilizar o conceito de resistência térmica.
Então, para a superfície , teremos:
E, essa resistência total pode ser escrita como a soma da resistência de condução e a de convecção, então, temos:
Substituindo os valores conhecidos, chegamos em:
E, agora, o fluxo de energia gerada por unidade de comprimento será a energia gerada no elemento combustível multiplicada pela área. Dessa forma, teremos:
Então, substituindo os valores encontrados na primeira equação do passo 1, temos:
Isolando :
Passo 3
Agora, como nós não temos fluxo de calor na superfície interna do elemento combustível, podemos escrever a equação para o perfil de temperatura conforme vimos nessa seção. Então, teremos:
E para descobrir a temperatura no ponto , vamos fazer :
E substituindo os valores conhecidos, temos:
Passo 4
Agora, para a letra (b), nós vamos partir da EDO radial com geração volumétrica:
Então, a solução que satisfaz a condição de fluxo nulo em é
Que também pode ser escrita na forma:
E, utilizando alguns valores de , chegamos nos seguintes perfis de temperatura:
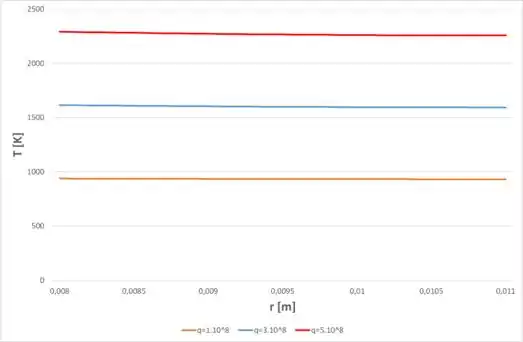
Passo 5
Para determinar o valor máximo permissível para , precisamos limitar a um valor :
Onde . Assim, vamos ter:
Valeu, galera! Até a próxima! 😉
Resposta
a),
b) ,