Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 66

Quatro superfícies difusas, que apresentam as características espectrais mostradas nas figuras, se encontram a 300 K e estão expostas à radiação solar.

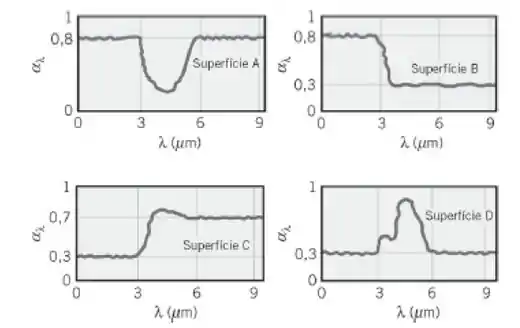
Quais das superfícies podem ser aproximadas como cinzas?

Passo 1

Vamos lá!! antes de mais nada precisamos fazer nossas famosas considerações. Hehe (u.u)

I - S u p e r f i c i e   é   d i f u s a

Esse problema é super simples, então vamos matar ele rapidinho para irmos para o próximo, vamos começar interpretando nosso problema.

Temos que para, λ = 3 μ m e T = 5800   K , λ T = 13.400   K ⋅ μ m , da tabela 12.1 F 0 → λ = 0,984 . O que nos indica que 98,4 % da radiação solar está na região espectral abaixo de 3   μ m .

E para λ = 6 μ m e T = 3 00   K , λ T = 1.800   K ⋅ μ m , da tabela 12.1 F 0 → λ = 0 , 039 . O que nos indica que 9 6 , 61 % da emissão da superfície está na região espectral acima de 6   μ m .

Passo 2

Com isso em mente, temos que uma superfície cinza é aquela que α λ e ε λ são constantes nas regiões espectrais de irradiação e de emissão da superfície, para os nossos exemplos temos:

S u p e r f í c i e   A   é   c i n z a , p o i s : α s ≈ ε = 0,8

S u p e r f í c i e   B   n ã o   é   c i n z a , p o i s : α s ≈ 0,8 ,   ε = 0,3

S u p e r f í c i e   C   n ã o   é   c i n z a , p o i s : α s ≈ 0 , 3 ,   ε ≈ 0 , 7

S u p e r f í c i e   D   é   c i n z a , p o i s : α s ≈ ε = 0 , 3

Isso é tudo pessoal! \o/

Resposta

S u p e r f í c i e   A   é   c i n z a , p o i s : α s ≈ ε = 0,8

S u p e r f í c i e   B   n ã o   é   c i n z a , p o i s : α s ≈ 0,8 ,   ε = 0,3

S u p e r f í c i e   C   n ã o   é   c i n z a , p o i s : α s ≈ 0,3 ,   ε ≈ 0,7

S u p e r f í c i e   D   é   c i n z a , p o i s : α s ≈ ε = 0,3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é efeito estufa? Por que é um assunto de grande preocupação entre os cientistas atmosféricos?
Podemos ver o interior de um forno de micro-ondas durante sua operação através da porta de vidro, o que indica que a radiação visível está escapando do forno. Você acha que a radiação nociva das micro
Uma bola de 13 cm de diâmetro esférico emite radiação a uma taxa de 140 W quando sua temperatura de superfície é 530 K. Determine a emissividade média da bola nessa temperatura.
53 – Uma chapa de aço emergindo de uma seção de laminação a quente tem uma temperatura de 1000 K, uma espessura de δ = 2,5 mm, e a seguinte distribuição de emissividade hemisférica espectral:A densida
35 – Um de dois revestimentos finos podem ser aplicados em uma placa metálica, produzindo as emissividades espectrais seguintes, abaixo e acima do comprimento de onda de corte, λc = 8 μm.Se a temperat