Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 60

Radiação deixa um forno, que tem temperatura superficial interna de 1500   K , através de uma abertura com 20   m m de diâmetro. Uma porção dessa radiação é interceptada por um detector que se encontra a uma distância de 1   m da abertura, tem uma área superficial de 10 – 5   m 2 e está orientado conforme ilustrado

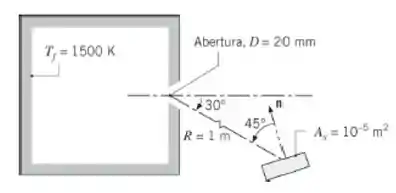
Se a abertura estiver aberta, qual é a taxa na qual a radiação que deixa o forno é interceptada pelo detector? Se a abertura estiver coberta com um material difuso e semitransparente cuja transmissividade espectral seja τ λ   =   0,8 para λ   ≤   2   μ m e τ λ   =   0 para λ   >   2   μ m , qual será a taxa na qual a radiação que deixa o forno é interceptada pelo detector?

Passo 1

Primeiro vamos fazer o gráfico da transmissividade espectral para ficar claro o comportamento da nossa radiação, para os dados da questão nosso gráfico vai ficar assim:

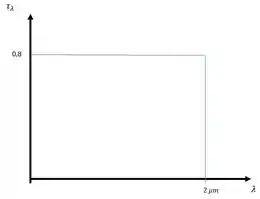
Vamos lá!! antes de mais nada precisamos fazer nossas famosas considerações. Hehe (u.u)

I - S u p e r f í c i e   d i f u s a

I I - A   e m i s s ã o   t e m   a s   m e s m a s   c a r a c t e r i s t i c a s   d e   u m a   e m i s s ã o   d e   c o r p o   n e g r o

I I I - A   a b e r t u r a   d o   f o r n o   e   n o s s o   d e c t e c t o r   s ã o   c o n s i d e r a d o s   i n f i n i t e s i m a i s

Passo 2

Agora vamos calcular a taxa radiativa que na superfície do receptor para a tampa do forno aberto, das equações 12.17 e 12.32 temos:

I e = E b T f π = σ T f 4 π = 5,67 ⋅ 10 - 8 ⋅ 1500 4 π   W m 2 ⋅ r a d

I e = 9,14 ⋅ 10 4   W m 2 ⋅ r a d

Da equação 12.7 :

ω s - a = A n r 2 = A s ⋅ cos ⁡ θ 2 r 2 = 10 - 5 ⋅ cos ⁡ 45 ° 1   m 2

ω s - a = 0,707 ⋅ 10 - 5   r a d

Calculando agora nossa taxa de calor, temos:

q = I e A a ω s - a cos ⁡ θ 1 = 9,14 ⋅ 10 4 ⋅ π 0,02 2 4 ⋅ 0,707 ⋅ 10 - 5 r a d ⋅ cos ⁡ 30 °

q = 1,76 ⋅ 10 - 4   W

Passo 3

Agora precisamos verificar o efeito da transmissividade espectral apresentada no passo 1 , assim temos da equação 12.61 .

τ = ∫ 0 ∞ α λ G λ d λ ∫ 0 ∞ G λ d λ = ∫ 0 ∞ ε λ E λ ,   b T f d λ ∫ 0 ∞ E λ ,   b d λ = 0,8 ∫ 0 0,2 E λ ,   b E b ⋅ d λ

τ = 0,8 ⋅ F 0 → 2 μ m

Onde λ T = 2   μ m ⋅ 1500 K = 3 000   μ m ⋅ K , assim da tabela 12.1 encontramos.

F 0 → 2 μ m = 0 , 273

Logo:

τ = 0,218

Agora calculando a taxa radiativa considerando o efeito da transmissividade espectral, temos:

q e s p e c = τ I e A a ω s - a cos ⁡ θ 1 = 0,218 ⋅ 1,76 ⋅ 10 - 4   W

q e s p e c = 0,384 ⋅ 10 - 4   W

Isso é tudo pessoal! \o/

Resposta

q = 1,76 ⋅ 10 - 4   W

q e s p e c = 0,384 ⋅ 10 - 4   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A vigia (com 50 mm de diâmetro) de uma grande fornalha operando a 450°C é coberta com um material que tem τ = 0,8 e ρ = 0 para a irradiação originada no interior da fornalha. O material tem uma emissi
A emissividade direcional espectral de um material difuso a 2000 K apresenta a seguinte distribuição: Determine a emissividade hemisférica total a 2000 K. Determine o poder emissivo na faixa espectral
Considere uma superfície difusa e opaca cuja refletividade espectral varia em função do comprimento de onda conforme ilustrado. A superfície se encontra a 750K e a irradiação sobre um dos seus lados v
Uma superfície difusa, que apresenta as características espectrais a seguir, é mantida a 500K quando localizada no interior de um grande forno cujas paredes são mantidas a 1500K :(a) Esboce a distribu
Um vidro difuso especial, com propriedades radiantes espectrais conhecidas, é aquecido no interior de um grande forno. As paredes do forno, que são mantidas a T p = 1800K , são revestidas com um tijol