Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 59
A emissividade espectral de uma superfície difusa e opaca é mostrada na figura.
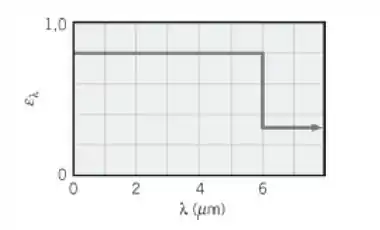
(a) Se a superfície for mantida a , qual é sua emissividade hemisférica total?
(b) Qual é a absortividade hemisférica total da superfície quando irradiada por uma grande vizinhança com emissividade de e temperatura de ?
(c) Qual é a radiosidade da superfície quando ela é mantida a e submetida à irradiação indicada na parte ?
(d) Determine o fluxo radiante líquido para a superfície nas condições da parte .
(e) Represente graficamente cada um dos parâmetros calculados nas partes como funções da temperatura da superfície para .
Passo 1
(a)
Vamos lá!! antes de mais nada precisamos fazer nossas famosas considerações. Hehe (u.u)
Agora vamos calcular a emissividade hemisférica, para uma temperatura de da equação temos:
Assim temos que:
Onde , assim da tabela encontramos.
Por fim nossa emissividade hemisférica é:
Passo 2
(b)
Vamos lá! Calculando a emissividade hemisférica para e vizinhança grande em relação ao meio onde .
Seguindo a lógica da letra (a), temos:
Onde , assim da tabela encontramos.
Por fim nossa emissividade hemisférica é:
Vale notar que para todas as situações onde a emissividade da vizinhança é desprezível.
Passo 3
(c)
Agora vamos calcular a radiosidade para uma superfície a e irradiado nas condições apresentadas no item (b), assim temos:
Passo 4
(d)
Vamos fazer um esqueminha do balanço de energia, vai ficar assim:
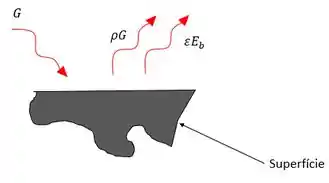
A fluxo radiante líquido na superfície é dado por:
Passo 5
(e)
Usando um programa podemos refazer a letra (a)-(d) variando a temperatura de superfície, teremos um arranjo de resultados que podemos explicitar em forma de gráfico, o arranjo vai ter a seguinte forma:
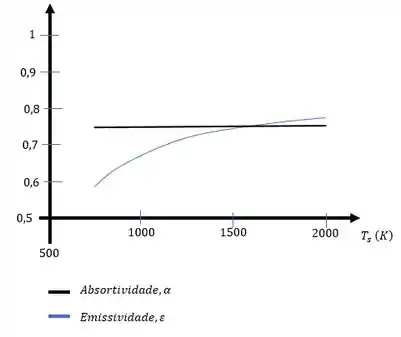
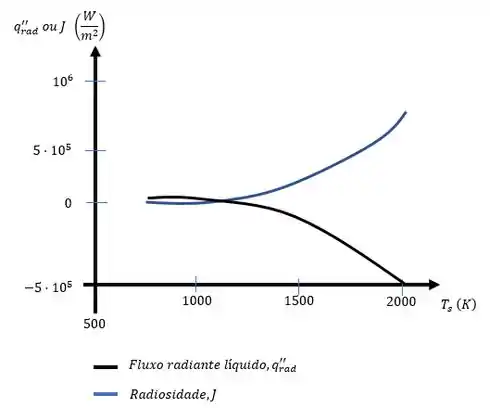
Isso é tudo pessoal! \o/
Resposta
(a)
(b)
(c)
(d)
(e) Gráficos vide passo a passo