Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 62

As transmissividades espectrais de vidros simples e vidros coloridos podem ser aproximadas como a seguir:

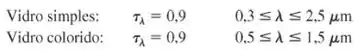
Fora dos intervalos de comprimentos de onda especificados, a transmissividade espectral para os dois tipos de vidro é igual a zero. Compare a energia solar que pode ser transmitida através dos vidros. Com irradiação solar sobre os vidros, compare a energia radiante visível que pode ser transmitida.

Passo 1

Vamos lá, antes de mais nada vamos traçar o diagrama da transmissividade espectral para os parâmetros apresentados.

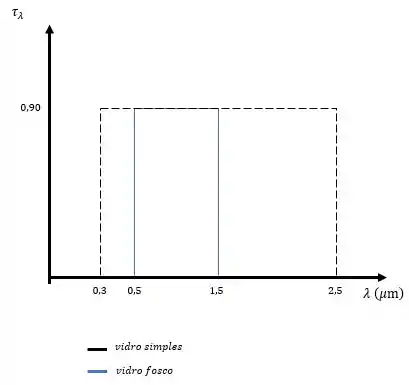
Vamos lá!! antes de mais nada precisamos fazer nossas famosas considerações. Hehe (u.u)

I - R a d i a ç ã o   é   p r o p r o c i o n a l   a   d e   u m   c o r p o   n e g r o   a   5800   K

Da equação 12.61 temos que a transmissividade global é dada por:

τ s = ∫ 0 ∞ τ λ G λ ,   s d λ ∫ 0 ∞ G λ ,   s d λ = ∫ 0 ∞ τ λ E λ ,   b λ , 5800   K d λ E b 5800   K

τ s = τ λ F λ 1 - λ 2 = τ λ F 0 - λ 2 - F 0 - λ 1

Agora só aplicarmos as condições dadas.

Passo 2

Vamos começar encontrando a irradiação solar sobre os vidros, pra encontrarmos F temos que usar a tabela 12.1 , vamos lá!

Para o vidro simples:

λ 1 = 0,3   μ m ,   λ 1 T = 0,3 ⋅ 5800 = 1.740   μ m ⋅ K

F 0 - λ 1 = 0,033

λ 2 = 2 , 5   μ m ,   λ 1 T = 2 , 5 ⋅ 5800 = 1 4 . 50 0   μ m ⋅ K

F 0 - λ 1 = 0 , 966

τ s ,   s = 0,9 0,966 - 0,033

τ s ,   s = 0,839

Para o vidro colorido:

λ 1 = 0 , 5   μ m ,   λ 1 T = 0 , 5 ⋅ 5800 = 2 . 90 0   μ m ⋅ K

F 0 - λ 1 = 0 , 250

λ 2 = 1 , 5   μ m ,   λ 2 T = 1 , 5 ⋅ 5800 = 8 . 7 00   μ m ⋅ K

F 0 - λ 2 = 0 , 881

τ s ,   c = 0,9 0,881 - 0,250

τ s ,   c = 0,568

Passo 3

Agora vamos encontrar a energia radiante visível que pode ser transmitida, pra encontrarmos F temos que usar a tabela 12.1 , vamos lá!

Os espectros visíveis variam de 0,4 até 0 , 7 para o vidro simples, e de 0 , 5 até 0 , 7 para o vidro pintado.

Para o vidro simples:

λ 1 = 0 , 4   μ m ,   λ 1 T = 0 , 4 ⋅ 5800 = 2 . 32 0   μ m ⋅ K

F 0 - λ 1 = 0 , 125

λ 2 = 0 , 7   μ m ,   λ 2 T = 0 , 7 ⋅ 5800 = 4 . 0 6 0   μ m ⋅ K

F 0 - λ 2 = 0 , 491

τ v i s ,   s = 0,9 0,491 - 0 , 329

τ v i s ,   s = 0,839

Para o vidro colorido:

λ 1 = 0,5   μ m ,   λ 1 T = 0,5 ⋅ 5800 = 2.900   μ m ⋅ K

F 0 - λ 1 = 0,250

λ 2 = 0,7   μ m ,   λ 2 T = 0,7 ⋅ 5800 = 4.060   μ m ⋅ K

F 0 - λ 2 = 0,491

τ v i s ,   s = 0,9 0,491 - 0,250

τ v i s ,   s = 217

Assim temos que a pintura do vidro reduz a irradiação solar em 32 % e a energia radiante visível que pode ser transmitida em 34 % !

Isso é tudo pessoal! \o/

Resposta

A pintura do vidro reduz a irradiação solar em 32 % e a energia radiante visível que pode ser transmitida em 34 % !

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas superfícies pequenas, A e B, estão localizadas no interior de um recipiente isotérmico a uma temperatura uniforme. O recipiente proporciona uma irradiação de 6300W / m 2 em cada uma das superfíci
Uma placa horizontal opaca tem uma espessura de λ=21m m e condutividade térmica de k=25W / ( m·K ) . Água escoa em contato com a superfície inferior da placa e está a uma temperatura de T ∞ , a g =25
Considere um material que é cinza, mas seletivo direcionalmente com α θ ( θ ,ϕ ) = 0 , 8 ( 1– cos ⁡ ϕ ) . Determine a absortividade hemisférica α quando um fluxo solar colimado irradia a superfície do
A emissividade direcional espectral de um material difuso a 2 5 00K apresenta a seguinte distribuição:Determine a emissividade hemisférica total a 2 5 00K . Determine o poder emissivo na faixa espectr
Um fluxo solar de 10 00W / m 2 incide sobre o lado superior de uma placa cuja superfície tem uma absortividade solar de 0,9 e uma emissividade de 0 , 2 . O ar e a vizinhança estão a 25 ° C , e o coefi