Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas Abrangentes - Ex. 7

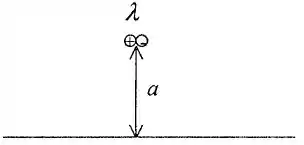
Encontre uma fórmula para a função corrente do escoamento de um dipolo de intensidade λ à distância “a” de uma parede, como na figura abaixo. (a) Trace as linhas de corrente. (b) Existem pontos de estagnação? (c) Encontre a velocidade máxima ao longo da parede e sua posição.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

Vamos usar um “dipolo imagem” de mesma intensidade e orientação, porém no ponto x , y = ( 0 , - a ) . A função de corrente para esse escoamento combinado vai formar uma “parede” em y = 0 entre os dois dipolos, certo?

ψ = - λ y + a x 2 + y + a 2 - λ y - a x 2 + y - a 2

Passo 2

(a) As linhas de corrente são mostradas abaixo para um dos quadrantes, uma vez que temos um campo de escoamento simétrico, pois ele é circular, parecido como na figura 8.8 do livro, mas ele é mais “ajustadinho” perto da parede por causa das condições de não deslizamento!

Passo 3

(b) Não há pontos de estagnação no campo de escoamento

Passo 4

(c) A velocidade ao longo da parede ( y = 0 ) é encontrada fazendo-se a diferencial da nossa equação de função de corrente!

u p a r e d e = ∂ ψ ∂ y ​ y = 0 = - λ x 2 + a 2 + 2 λ a 2 x 2 + a 2 - λ x 2 + a 2 + 2 λ a 2 x 2 + a 2 2  

A velocidade máxima acontece quando x = 0 , ou seja, exatamente entre os dois dipolos!!!

u p a r e d e ,   m á x = 2 λ a 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o campo de escoamento formado pela combinação de um escoamento uniforme no sentido positivo de x e um sorvedouro localizado na origem. Seja U = 50m / s e q = 90m 2 / s . Use um volume de con
Mostre que qualquer função diferenciável f ( z ) do número complexo z = x + i y conduz a um potencial válido (a parte real de f ) e a uma função de corrente correspondente (a parte negativa imaginária
Considere o campo de escoamento representado pelo potencial de velocidade φ = A x + B x 2 - B y 2 , em que A = 1 m - 1 . s - 1 , B = 1 m - 1 . s - 1 e as coordenadas são medidas em metros. Obtenha exp
Considere o campo de escoamento formado pela combinação de um escoamento uniforme no sentido positivo de x e uma fonte localizada na origem. Seja U = 30m / s e q = 150m 2 / s . Trace um gráfico da raz
O que significa quando dizemos que duas ou mais equações diferenciais são acopladas?