Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 103
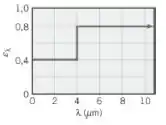
Um revestimento fino, que é aplicado sobre longos bastões cilíndricos de cobre com de diâmetro, é curado pela colocação dos bastões, em posição horizontal, no interior de um grande forno cujas paredes são mantidas a . No interior do forno há nitrogênio gasoso, que também se encontra a e a uma pressão de . O revestimento é difuso e sua emissividade espectral tem a distribuição mostrada na figura.
(a) Quais são a emissividade e a absortividade dos bastões revestidos quando sua temperatura é de ?
(b) Qual é a taxa inicial de variação da temperatura dos bastões?
(c) Quais são a emissividade e a absortividade dos bastões revestidos quando eles atingem a temperatura do regime estacionário?
(d) Estime o tempo necessário para que a temperatura dos bastões atinja .
Passo 1
Nessa questão nós temos as propriedades radiativas espectrais do revestimento fino aplicadas a hastes de cobre circulares longas de diâmetro e temperatura prescritos. Condições de parede e atmosfera do forno em que as hastes são inseridas.
Com isso vamos encontrar a emissividade e absortividade das hastes revestidas quando a temperatura é , a taxa inicial de variação de temperatura, e a emissividade e absortividade quando atingem a temperatura em estado estacionário, show? Vamos lá!
Passo 2
Para resolver essa questão vamos assumir que:
(1) A temperatura da haste é uniforme;
(2) O nitrogênio é quiescente;
(3) Propriedades constantes;
(4) Revestimento superficial difuso e opaco;
(5) As paredes do forno formam uma cavidade de corpo negro em torno dos cilindros,
(6) Efeitos finais insignificantes.
A emissividade total da barra de cobre, , em pode ser expresso em termos do fator de emissão da banda,
Usando a tabela 12.1 para
A absorção total, , para irradiação para as paredes do forno a , é
Usando a tabela 12.1 para
Passo 3
De um balanço de energia em um volume de controle sobre a haste,
Com,
A correlação Churchill-Chu do capítulo 9 gera,
Com os valores de e da parte (a), a taxa de mudança de temperatura com o tempo é,
Passo 4
Sob condições de estado estacionário, Para esta situação, , portanto,
O tempo necessário para que as hastes, inicialmente em , atinjam podem ser determinadas usando o método da capacitância concentrada.
Utilização do Modelo de Capacitância IHT Lumped, considerando processos de convecção, irradiação e emissão; a ferramenta Correlações, convecção livre, cilindro horizontal; Ferramenta de Radiação, Frações de Emissão de Banda; e uma função de tabela de pesquisa gerada pelo usuário para as propriedades termofísicas de nitrogênio, encontramos:
Resposta
- e