Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 23
Repita o Problema 6-22 para o caso de outro cotovelo (idêntico) anexado ao cotovelo existente, para que o fluido faça uma volta em U.
Passo 1
O exercício quer que a gente calcule para a volte em U tudo o que a gente calculou para o cotovelo. Ou seja, ele quer que a gente calcule primeiro a pressão manométrica da linha de corrente central da entrada da volta em U. Depois, ele quer que a gente a força que faz a volta em U ficar parado. Essa força tem duas componentes: a componente horizontal (do eixo ) e a componente vertical (do eixo ) . A figura abaixo mostra a linha de corrente central da volta em U e alguns dados fornecidos pelo enunciado.
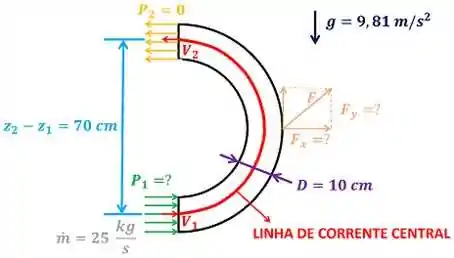
é o diâmetro da seção transversal da volta em U. é a pressão manométrica linha de corrente central da saída da volta em U. Ela vale zero, porque é igual à pressão atmosférica. é a velocidade de entrada da água e é a velocidade de saída da água. é a diferença de altitude entre a entrada e a saída da volta em U. é a vazão de água através da volta em U. é a componente horizontal e é a componente vertical da força que faz a volta em U ficar parado. é a aceleração da gravidade.
Para encontrar de forma mais fácil temos que entender uma informação que o enunciado esconde da gente e temos que fazer algumas simplificações. No próximo passo faremos isso.
Passo 2
Quando o enunciado da questão 6-22 fala que o cotovelo é usado para direcionar o escoamento da água a uma taxa de , ele quer dizer que a vazão de entrada de água é igual à vazão de saída! Isso também serve para a volta em U! Isso é uma forma do enunciado dizer que o escoamento de água está em regime permanente.
Além disso, para diminuir as contas que a gente precisa fazer podemos fazer algumas simplificações. Podemos considerar que a água é incompressível ( constante através do escoamento), sem atrito e irrotacional (vorticidade vale zero em todo o escoamento). Fazendo todas essas simplificações, podemos usar a equação de Bernoulli na linha de corrente central do escoamento de para calcular .
onde é a densidade da água.
Podemos calcular e através da fórmula de vazão.
Pelas fórmulas de e , podemos notar que as duas velocidades são iguais. Substituindo isso na fórmula e lembrando que é nulo, achamos:
Passo 3
Substituindo os dados na fórmula de , achamos o valor dessa pressão. No entanto, antes disso precisamos converter de centímetro para metro .
Também precisamos considerar que a densidade da água vale . Esse é o valor da densidade da água na pressão atmosférica e na temperatura ambiente!
Passo 4
Para calcular as forças e que são necessárias para manter a volta em U sem se mover horizontalmente e verticalmente, vamos adaptar a equação do livro (segunda lei de Newton) para o nosso caso.
onde é o somatório das forças horizontais (no eixo ) sobre o volume de controle, é o fator de correção para o escoamento que entra no volume de controle. é o fator de correção para o escoamento que sai do volume de controle. Esses dois fatores de conversão valem segundo o enunciado.
é a velocidade da água no eixo entrando na volta em U. é a velocidade da água no eixo saindo da volta em U. A velocidade é horizontal pra esquerda. Logo, sua componente horizontal vale . Além disso, a velocidade também é horizontal. Logo, sua componente horizontal é igual à .
As forças do eixo são apenas as forças que as pressões e exercem sobre a entrada e a saída da volta em U e a força . Como as três forças têm o mesmo sentido (da esquerda para a direita), a força resultante é igual à soma entre as forças das pressão e e .
Substituindo isso na equação anterior, encontramos:
Passo 5
Para encontrar temos que adaptar a equação de .
onde é o somatório das forças verticais (no eixo ) sobre o volume de controle.
é a velocidade da água no eixo entrando na volta em U. é a velocidade da água no eixo saindo da volta em U. A velocidade é horizontal. Logo, sua componente vertical é igual a zero . Além disso, a velocidade também é horizontal. Logo, sua componente vertical vale zero .
Já as forças do eixo é apenas a força .
Substituindo isso na equação anterior, encontramos:
Passo 6
Substituindo os dados na fórmula de somos capazes de encontrar o valor dessa componente da força total . No entanto, antes disso precisamos converter de centímetro para metro .
Para calcular total, fazemos a soma dos quadrados dos componentes e depois aplicamos a raiz quadrada.