Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 19

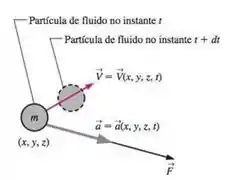
No Capítulo 4 definimos a aceleração material, que é a aceleração quando acompanhamos uma partícula de fluido (Figura P7-19),

α → ( x , y , z , t ) = ∂ V → ∂ t + ( V → ⋅ ∇ → ) V →

(a) Quais são as dimensões primárias do operador gradiente V?

(b) Certifique-se de que cada termo aditivo da equação tenha as mesmas dimensões.

Passo 1

Oi pessoal, tudo bem?

Bem, inicialmente, por definição, o operador de gradiente é um operador derivado tridimensional. Por exemplo, em coordenadas cartesianas, o operador de gradiente em coordenadas cartesianas é:

∇ → = ∂ ∂ x , ∂ ∂ y , ∂ ∂ z = i → ∂ ∂ x + j → ∂ ∂ y + k → ∂ ∂ z         ( 1 )

Passo 2

Letra a) Agora, vamos descobrir as dimensões primárias do operador gradiente V:

Como estamos tratando de aceleração material, devemos lembrar que cada membro da equação deve ter como medida:

m s 2

Observando o membro " ( V → ⋅ ∇ → ) V → " , percebemos que, o produto escalar fica:

m s ⋅ ∇ → ⋅ m s = m s 2           → ∇ →   = 1 m o u   1 c o m p r i m e n t o

Obs: Poderíamos encontrar também a relação 1 c o m p r i m e n t o a partir da definição mostrada na eq. 1.

Passo 3

Letra b) Da mesma forma, as dimensões primárias de uma derivada do tempo ( ∂ / ∂ t ) são 1 / t e m p o . Além disso, as dimensões primárias da velocidade são comprimento/tempo e as principais dimensões da aceleração são comprimento/tempo². Assim, cada termo na equação dada pode ser escrito em termos de dimensões primárias:

a = m s 2 = c o m p r i m e n t o t e m p o 2           ∂ V → ∂ t = m s s = c o m p r i m e n t o t e m p o 2         V → ⋅ ∇ → V → = m s ⋅ 1 m ⋅ m s = c o m p r i m e n t o t e m p o 2    

Resposta

Letra a) ∇ →   = 1 m o u   1 c o m p r i m e n t o

Letra b) a = m s 2 = c o m p r i m e n t o t e m p o 2           ∂ V → ∂ t = m s s = c o m p r i m e n t o t e m p o 2         V → ⋅ ∇ → V → = m s ⋅ 1 m ⋅ m s = c o m p r i m e n t o t e m p o 2    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em 1851, Sir George Stokes formulou a teoria de que a força de arrasto F sobre uma partícula em um escoamento de alta viscosidade (número de Reynolds baixo) depende somente da viscosidade m, da veloci
A Figura P1.14 mostra o escoamento da água sobre uma barragem. Sabe-se que a vazão em volume Q depende somente da largura da soleira B , da aceleração da gravidade g e da altura da lâmina d’água a mon
Equações algébricas como a relação de Bernoulli, Equação (1) do Exemplo 1.3, são dimensionalmente consistentes, mas e as equações diferenciais? Considere, por exemplo, a equação da quantidade de movim
A fórmula Stokes-Oseen [33] para a força de arrasto F sobre uma esfera de diâmetro D em uma corrente de fluido de baixa velocidade V , massa específica ρ e viscosidade μ é F = 3 π μ D V + 9 π 16 ρ V 2
A fórmula de Hazen-Williams da hidráulica para a vazão em volume Q em um tubo de diâmetro D e comprimento L é dada por Q ≈ 61,9 D 2,63 Δ p L 0,54 em que Δ p é a queda de pressão requerida para manter