Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 149

Ar escoa a 3,0 ao redor de um aerofólio em formato de losango duplamente simétrico cujos ângulos inclusos dianteiro e traseiro são ambos de 24º. Para ângulo de ataque nulo, calcule o coeficiente de arrasto pela teoria de choque e expansão e compare com a teoria de Ackeret.

Passo 1

Bora pra mais uma!

O aerofólio e suas pressões frontal e traseira são mostradas segundo desenho abaixo, onde os dados são obtidos com a tabela B, basta encontrar e somar o ângulo de giro para encontrar o novo numero de Mach e suas pressões:

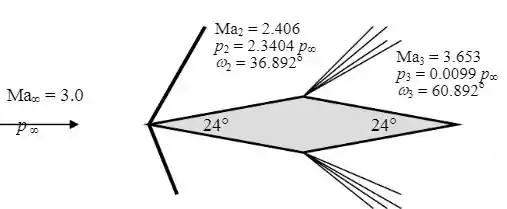
A espessura do aerofólio é igual a E o coeficiente de arrasto é:

Agora, pela teoria de Ackeret, Equação 9.107, o coeficiente de arrasto previsto é um pouco menor:

Resposta

Pela teoria do choque e expansão e pela teoria de Ackeret Essa diferença de 19% no valor, se deve ao fato do aerofólio ser muito espesso.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

The Beechcraft T-34C aircraft has a gross weight of5500 lbf and a wing area of 60 ft2 and fl ies at 322 mi/h at10,000-ft standard altitude. It is driven by a propeller thatdelivers 300 hp to the air.

The world’s largest airplane, the Airbus A380, has a maximum weight of 1,200,000 lbf, wing area of 9100 ft2, wingspan of 262 ft, and CDo 5 0.026. When cruising atmaximum weight at 35,000 ft, the four

Consider a fl at-plate airfoil at an angle of attack of 68. TheMach number is Ma` 5 3.2 and the stream pressure p` isunspecified. Calculate the predicted lift and drag coefficientsby (a) shock-expansi

The F-22 supersonic fi ghter cruises at 11,000 m altitude,with a weight of 50,000 lbf and thrust of 10,000 lbf. Itswing area is 840 ft2. Assume the wing is a 6-percent-thickdiamond shape and provides

The X-43 model A scramjet aircraft in Fig. C9.8 is smallW 5 3000 lbf, and unmanned, only 12.33 ft long and 5.5 ftwide. The aerodynamics of a slender arrowhead-shapedhypersonic vehicle is beyond our sc