Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 119
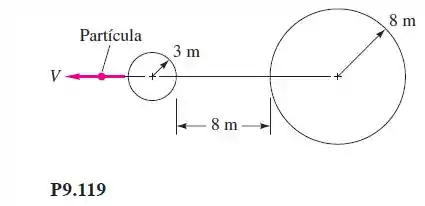
A partícula na Figura P9.119 está se movendo supersonicamente no ar padrão ao nível do mar. Das duas esferas de perturbação dadas, calcule o número de Mach, a velocidade e o ângulo de Mach da partícula.
Passo 1
Bora pra mais uma!
Se o ponto “a” representa t=0 unidades, a partícula atinge o ponto “b” em 8-3=5 unidades. Mas, a distância de “a” até “b” é 8+8+3=19 unidades. Portanto, o numero de Mach é subsônico e é:
Daí, a velocidade da partícula é:
Por fim, para calcular o Angulo de Mach, fazemos a função arco seno para obter:
Resposta
O número de Mach é 3,8 e resulta em um ângulo de e a velocidade da partícula é 1290m/s.
Exercícios de Livros Relacionados
Uma sonda estática de Pitot é usada para medir a velocidade de um avião que voa a 3000m . Se a leitura da pressão diferencial for de 3k P a , determine a velocidade do avião.
Um piezômetro e um tubo de Pitot são colocados em uma tubulação de água horizontal com 3c m de diâmetro, e a altura das colunas d'agua são medidas como 20c m no piezômetro e 35c m no tubo de Pitot (am
Um tanque pressurizado de água tem um orifício de 10c m de diâmetro na parte inferior, onde a água é descarregada para a atmosfera. O nível da água está 3m acima da saída. A pressão do ar do tanque ac
O diâmetro de um tanque de água cilíndrico é D 0 e sua altura é H . O tanque é enchido com água e está aberto para a atmosfera. Um orifício de diâmetro D com uma entrada uniforme (ou seja, sem perdas)
Um avião voa a uma altitude de 12.000 m . Determine a pressão manométrica no ponto de estagnação no nariz do avião se a velocidade for de 200k m / h . Como você solucionaria este problema para uma vel